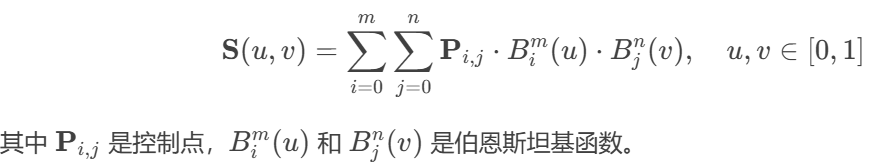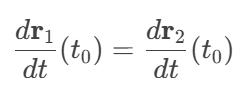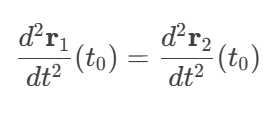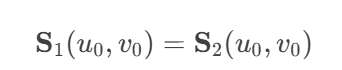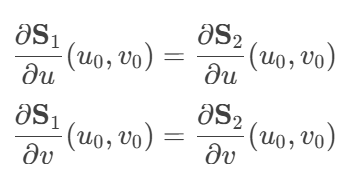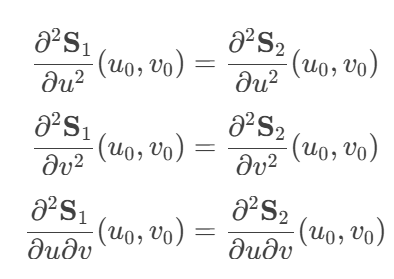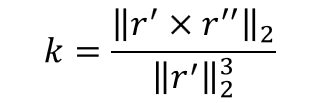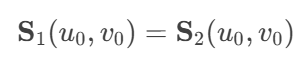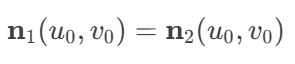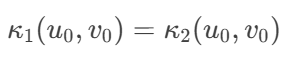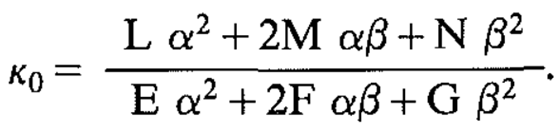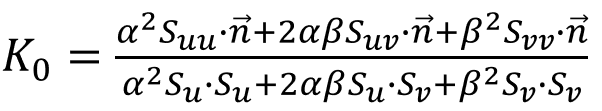定义

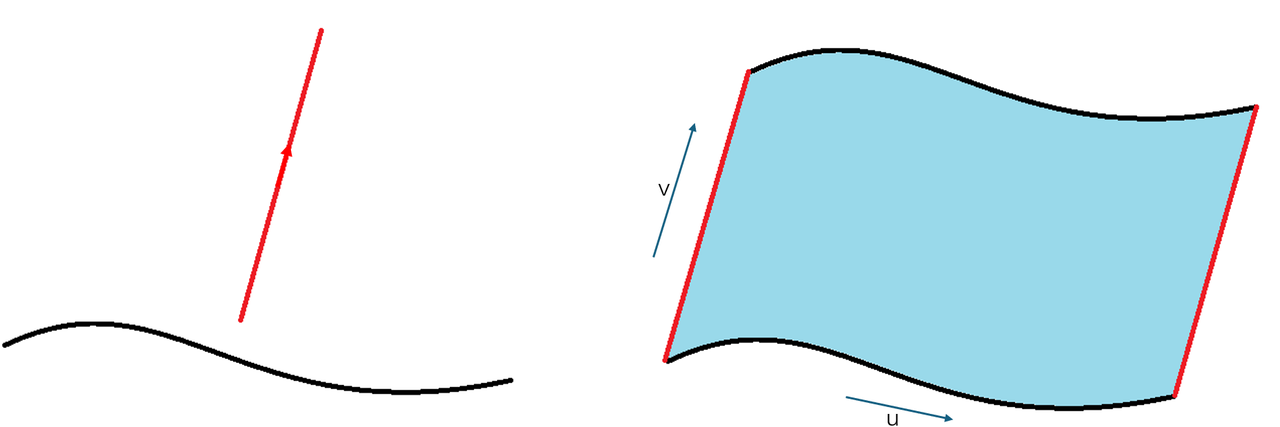
参数曲线

参数曲线是通过一个参数 t 来描述的曲线，通常表示为：C(t) = (x(t),y(t),z(t))。其中：t 是参数，通常定义在某个区间 [a,b] 上。x(t)、y(t)、z(t) 是关于参数 t 的函数，分别表示曲线在三维空间中的坐标。参数曲线通过参数 t 的变化来描述曲线的形状。因为参数化方式不唯一，所以同一个曲线可以用不同的参数方程表示。
接下来我们将举一些例子。

直线： C(t) = P0 + t⋅(P1−P0) , t∈[0,1]，其中 P0 和 P1 是直线的起点和终点。
圆弧： C(t) = (rcos(t),rsin(t)) , t∈[0,2π]，其中 r 是半径。
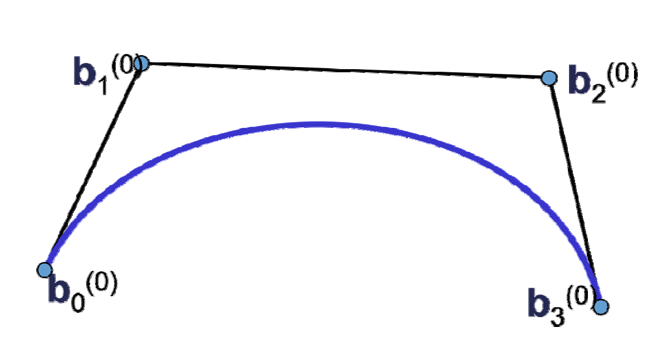
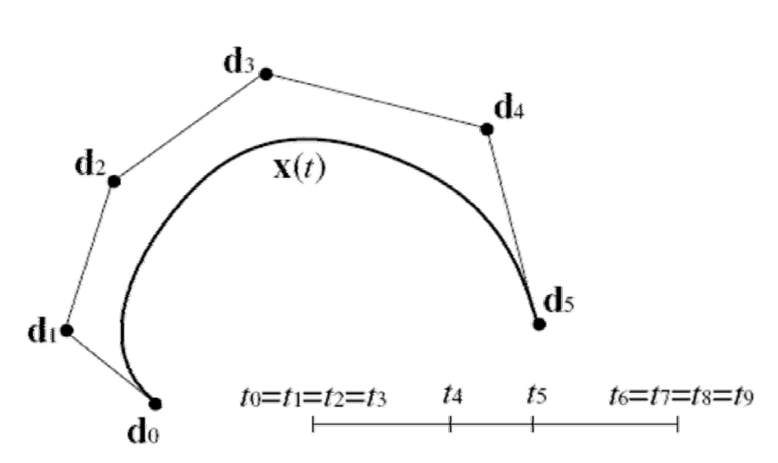
贝塞尔曲线：

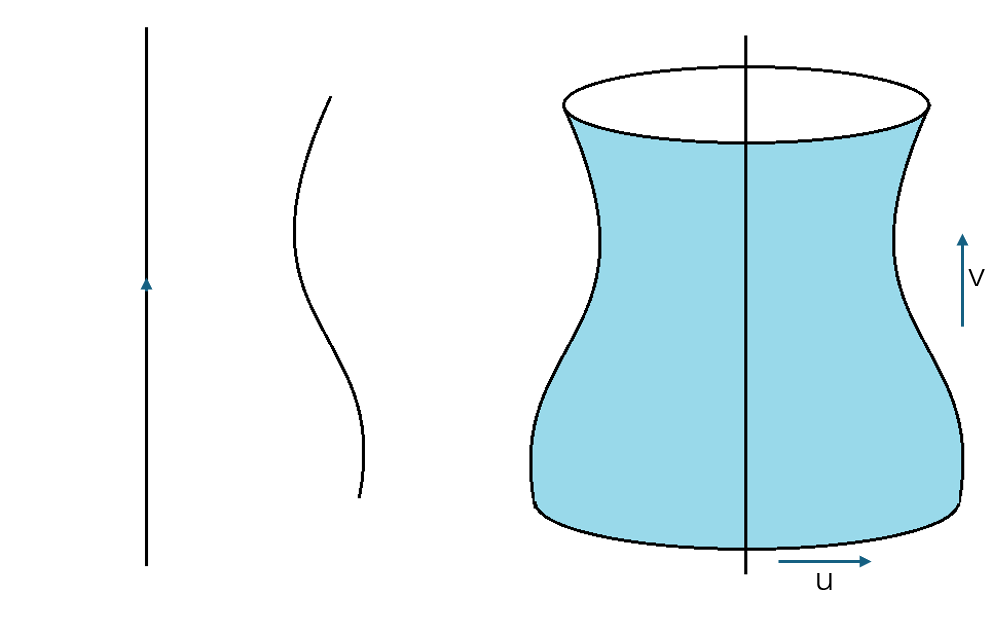
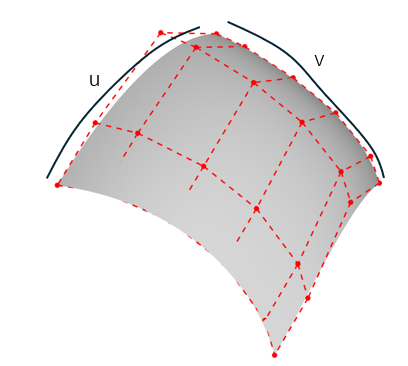
参数曲面

参数曲面是通过两个参数 u 和 v 来描述的曲面，通常表示为：S(u,v) = (x(u,v),y(u,v),z(u,v))，其中 u 和 v 是参数，通常定义在某个区域 [a,b]×[c,d] 上，x(u,v)、y(u,v)、z(u,v) 是关于参数 u 和 v 的函数，分别表示曲面在三维空间中的坐标。参数曲面通过参数 u 和 v 的变化来描述曲面的形状。因为参数化方式不唯一，所以同一个曲面可以用不同的参数方程表示。
接下来我们将举一些例子。

平面： S(u,v) = P0 + u⋅A + v⋅B, u, v∈R。其中 P0是平面上的一个点，A 和 B 是平面的两个方向向量。
球面： S(u,v) = (rsin(u)cos(v),rsin(u)sin(v),rcos(u)) ,u∈[0,π],v∈[0,2π]。其中 r 是半径。
贝塞尔曲面：

连续性

参数连续

曲线

参数连续是指曲线在连接处的参数导数连续。对于曲线来说，参数连续性涉及一阶导数、二阶导数等高阶导数。在 CAD 和几何建模中，参数连续用于确保曲线拼接的光滑性。高阶参数连续（如 C²）常用于汽车、航空航天等领域，要求曲线的曲率连续。

定义

C⁰ 连续：曲线在连接点处位置连续，但切线方向可能不连续。
C¹ 连续：曲线在连接点处位置和一阶导数（切线方向）连续。
C² 连续：曲线在连接点处位置、一阶导数和二阶导数（曲率）连续。

条件

对于两条曲线 r1(t) 和 r2(t)，在连接处 t=t0 需要满足：

C⁰ 连续：r1(t0) = r2(t0)
C¹ 连续：
C² 连续：

曲面

参数连续是指曲面在连接处的参数导数连续。对于曲面来说，参数连续性不仅涉及 u 和 v 方向的一阶导数，还涉及高阶导数。在 CAD 和几何建模中，参数连续用于确保曲面拼接的光滑性。高阶参数连续（如 C²）常用于汽车、航空航天等领域，要求曲面的曲率连续。

定义

C⁰ 连续：曲面在连接处位置连续，但法向量可能不连续。
C¹ 连续：曲面在连接处位置和一阶偏导数（切平面）连续。
C² 连续：曲面在连接处位置、一阶偏导数和二阶偏导数（曲率）连续。

条件

对于两个曲面 S1(u,v) 和 S2(u,v)，在连接处需要满足：

C⁰ 连续：
C¹ 连续：
C² 连续：

几何连续

曲线

几何连续是指曲线在连接处的几何性质（如切线方向、曲率）连续，而不一定要求参数导数连续。几何连续更注重曲线的视觉效果。几何连续的条件比参数连续宽松，因此在某些情况下更容易实现。

定义

G⁰ 连续：曲线在连接点处位置连续，但切线方向可能不连续。
G¹ 连续：曲线在连接点处位置连续，且切线方向连续（切线方向相同，但大小可能不同）。
G² 连续：曲线在连接点处位置和切线方向连续，且曲率连续（曲率相同，但曲率变化率可能不同）。

条件

对于两条曲线 r1(t) 和 r2(t)，在连接处 t=t0 需要满足：

G⁰ 连续：r1(t0) = r2(t0)
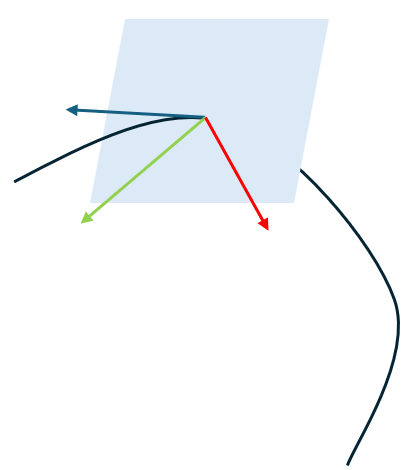
G¹ 连续：T1(t0) || T2(t0)，其中 T1 和 T2 是曲线的单位切向量
G² 连续：κ1(t0) = κ2(t0)，其中 κ1 和 κ2 是曲线的曲率

在上面我们提到了曲率，参数曲线的曲率的计算公式为：

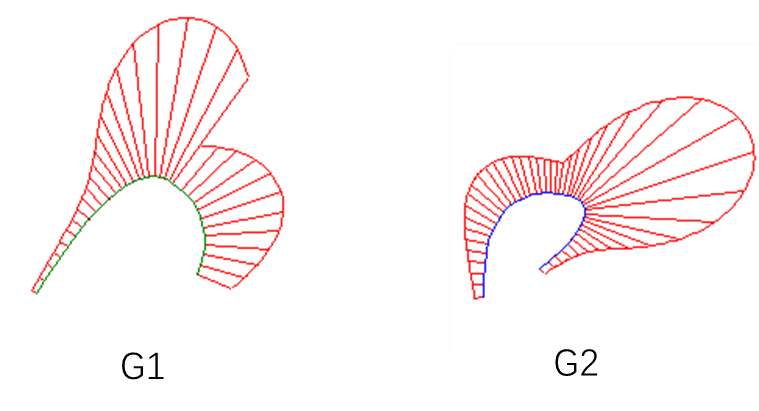
在商用软件中可以查看曲线的曲率梳，曲率连续即为 G2：

曲面

几何连续是指曲面在连接处的几何性质（如切平面、曲率）连续，而不一定要求参数导数连续。几何连续更注重曲面的视觉效果。几何连续的条件比参数连续宽松，因此在某些情况下更容易实现。

定义

G⁰ 连续：曲面在连接处位置连续，但法向量可能不连续。
G¹ 连续：曲面在连接处位置连续，且法向量连续（切平面相同，但切向量的长度可能不同）。
G² 连续：曲面在连接处位置和法向量连续，且曲率连续（所有法曲率相同，但曲率变化率可能不同）。

条件

对于两个曲面 S1(u,v) 和 S2(u,v)，在连接处需要满足：

G⁰ 连续：
G¹ 连续：

其中 n1 和 n2 是曲面的法向量。
G² 连续：

其中 κ1 和 κ2 是曲面的曲率。

在这里补充一些内容：
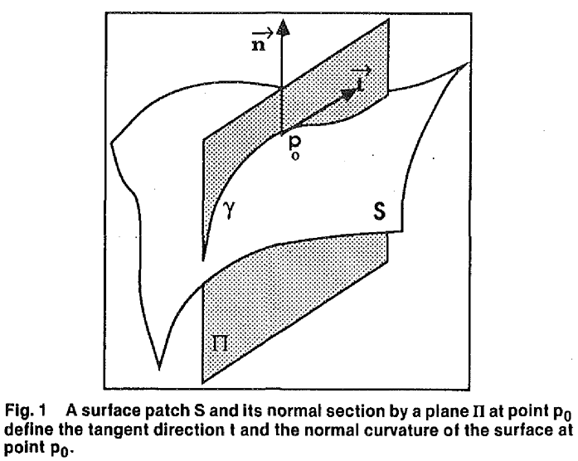
1.法曲率定义
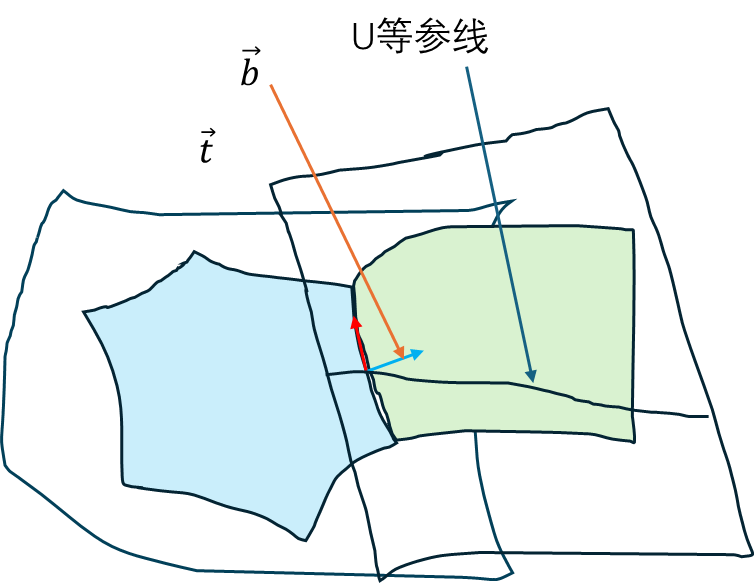
法曲率定义为曲面和某一法平面（过法向的平面）交线的曲率，如下图所示。图中曲线 γ 在 p0 点处的曲率即曲面 S 在 p0 处 t 方向的法曲率。

法曲率的定义并不易于计算。计算法曲率的简便方法为：计算方向 t 在切平面上的坐标，记为 (α,β)，即 t=αDu + βDv，则法曲率为：

其中，EFG 与曲面第一基本型中的符号含义相同；LMN 与曲面第二基本型中的符号含义相同，即：

2.G2 连续即在连接曲线上任一点的所有方向法曲率都相同

但是所有方向法曲率都相同是非常强的条件，Link Curvage Theorem 证明了，只需在 1 个与 t 不共线的方向上法曲率相等，那么所有方向上的法曲率都相等。所以只考虑 t 的法向 b，只要 b 方向的法曲率是相同的，那么就 G2 连续。

3.曲面 G2 连续的表现
曲面是否 G2 连续可以通过光学效果进行近似分析。G0 的斑马线是断开的，G1 的斑马线相连但不光滑，G2 的斑马线相连且光滑。

更为实用的几何连续性表达

从上述几何连续性的定义可以推导出一些更具实用价值的结论：

1. 曲线 a 在和曲线 b 的连接点处一阶导为 d1，二阶导为 d2，若曲线 b 在连接点处一阶导为 a*d1，则 G1 连续；若曲线 b 一阶导为 a*d1 并且二阶导为 a*a*d2+b*d1，则 G2 连续，其中 a 为非负实数，b 为实数。该结论使得曲线 G2 连续可以用两个参数进行控制，并且实现方式为 C2。
2. 曲面 a 和曲面 b 在 u 边界相连且 G1 连续，曲面 a 在和曲面 b 的某一连接点处的 u 方向 1 阶导为 du，二阶导为 duu，若曲面 b 在连接点处的 u 方向一阶导为 a*du 并且二阶导为 a*a*duu + b*du，则 G2 连续，其中 a 为非负实数，b 为实数。该结论使得曲面在边界处的G2连续可以用两个参数进行控制，并且实现方式为 C2。

二维参数曲线

常见功能

获得参数范围

AMCAX::Geom2Curve::FirstParameter 用于获得曲线的起始参数， AMCAX::Geom2Curve::LastParameter 用于获得曲线的终止参数。

//1
//Make a 2D BSplineCurve
std::vector<AMCAX::Point2> pts22 = {
   AMCAX::Point2(0.5, 0.5),
   AMCAX::Point2(1.0, 3.0),
   AMCAX::Point2(3.0, 1.0),
   AMCAX::Point2(3.8,2.0),
   AMCAX::Point2(2.5,3.5),
   AMCAX::Point2(1.0,0.5),
   AMCAX::Point2(0.3,2.0)
};
std::vector<double> knots = { 0.0, 0.25, 0.5,0.75,1.0 };
std::vector<int> mults = { 4, 1, 1,1,4 };
std::shared_ptr< AMCAX::Geom2BSplineCurve> bspline2 = std::make_shared< AMCAX::Geom2BSplineCurve>(pts22, knots, mults, 3);
//Get the FirstParameter and LastParameter
double fp = bspline2->FirstParameter();
double lp = bspline2->LastParameter();
std::cout << fp <<"," << lp << std::endl;//0,1
//2
//Make a trimcurve
std::shared_ptr< AMCAX::Geom2Parabola >parabola2 = std::make_shared< AMCAX::Geom2Parabola>(AMCAX::Frame2(), 2.0);
AMCAX::Geom2TrimmedCurve trimcurve(parabola2, -2.0, 2.0);
//Get the FirstParameter and LastParameter
double fp2 = trimcurve.FirstParameter();
double lp2 = trimcurve.LastParameter();
std::cout << fp2 << "," << lp2 << std::endl;//-2,2

求值和求导

AMCAX::Geom2Curve::Value 或 AMCAX::Geom2Curve::D0 用于求值，而 AMCAX::Geom2Curve::D1 ， AMCAX::Geom2Curve::D2 ， AMCAX::Geom2Curve::D3 ， AMCAX::Geom2Curve::DN 用于求导。

//1
//Value
double t = 0.4 * (fp + lp);
AMCAX::Point2 p1 = bspline2->Value(t);
//D0 D1 D2 D3 DN
AMCAX::Point2 p2;
AMCAX::Vector2 d1, d2, d3;
bspline2->D0(t, p2);
bspline2->D1(t, p2, d1);
bspline2->D2(t, p2, d1, d2);
bspline2->D3(t, p2, d1, d2, d3);
int deriv = 4;
AMCAX::Vector2 dn = bspline2->DN(t, deriv);
 
//2
//Value
double t2 = 1.5;
AMCAX::Point2 p3 = trimcurve.Value(t2);
//D0 D1 D2 D3 DN
AMCAX::Point2 p4;
AMCAX::Vector2 dd1, dd2, dd3;
trimcurve.D0(t2, p4);
trimcurve.D1(t2, p4, dd1);
trimcurve.D2(t2, p4, dd1, dd2);
trimcurve.D3(t2, p4, dd1, dd2, dd3);
int deriv2 = 4;
AMCAX::Vector2 ddn = trimcurve.DN(t2, deriv2);

获得类型

AMCAX::Geom2Curve::Type 用于获得曲线类型，如直线、圆、椭圆、抛物线等。曲线类型可参考枚举类 CurveType 。

std::cout << int(bspline2->Type()) << ";" << int(trimcurve.Type());//7;8

封闭性、周期性

AMCAX::Geom2Curve::IsClosed 用于获得曲线的封闭性（起始点与终止点是同一个点）， AMCAX::Geom2Curve::IsPeriodic 用于获得曲线的周期性。

std::cout <<bspline2->IsClosed()<< ";" << bspline2->IsPeriodic();//0;0

std::cout <<trimcurve.IsClosed()<< ";" << trimcurve.IsPeriodic();//0;0

反向

AMCAX::Geom2Curve::Reverse 用于将 Geom2Curve 反向，改变自身，而 AMCAX::Geom2Curve::Reversed 用于获取反向的 Geom2Curve，不改变自身。反转后，曲线的起点和终点发生了对换。对于一般曲线，曲线参数范围不变，而对于裁剪曲线，可能会改变曲线的参数范围。如以下例子，一条裁剪直线原来的参数范围为 -1 到 3，反转后变为 -3 到 1。

//1
std::vector<AMCAX::Point2> pts3 = {
   AMCAX::Point2(0.0, 0.0),
   AMCAX::Point2(2.0, 2.0),
   AMCAX::Point2(4.0, 3.0),
};
auto bezier2 = std::make_shared<AMCAX::Geom2BezierCurve>(pts3);
std::cout << bezier2->FirstParameter() << std::endl;//0
std::cout << bezier2->LastParameter() << std::endl;//1
//  reversed
auto reversebezier = bezier2->Reversed();
std::cout << reversebezier->FirstParameter() << std::endl;//0
std::cout << reversebezier->LastParameter() << std::endl;//1
std::cout << reversebezier->Value(0) << std::endl;//4 3
std::cout << reversebezier->Value(1) << std::endl;//0 0
 
//reverse
bezier2->Reverse();
std::cout << bezier2->FirstParameter() << std::endl;//0
std::cout << bezier2->LastParameter() << std::endl;//1
std::cout << bezier2->StartPoint() << std::endl;//4 3
std::cout << bezier2->EndPoint() << std::endl;//0 0
 
//2
auto line2 = std::make_shared<AMCAX::Geom2Line>(AMCAX::Point2(0., 0.), AMCAX::Direction2(1., 0.));
auto trimline2 = std::make_shared<AMCAX::Geom2TrimmedCurve>(line2, -1., 3.);
std::cout << trimline2->StartPoint() << std::endl;//-1 0
std::cout << trimline2->EndPoint()<< std::endl;//3 0
//  reversed
auto reverseline = trimline2->Reversed();
std::cout << reverseline->FirstParameter() << std::endl;//-3
std::cout << reverseline->LastParameter() << std::endl;//1
std::cout << reverseline->Value(-3) << std::endl;//3 0
std::cout << reverseline->Value(1) << std::endl;//-1 0
 
//reverse
trimline2->Reverse();
std::cout << trimline2->FirstParameter() << std::endl;//-3
std::cout << trimline2->LastParameter() << std::endl;//1
std::cout << trimline2->StartPoint() << std::endl;//3 0
std::cout << trimline2->EndPoint() << std::endl;//-1 0

在这里我们解释一下反转后，裁剪直线的参数范围变为 -3 到 1 的原因，这是因为裁剪曲线在反转的时候是先对其 basiscurve （无穷长的直线）做反转，然后再根据裁剪起始点和终止点的参数确定反转后的参数。

另外如果想计算某一参数的对称参数可通过 AMCAX::Geom2Curve::ReversedParameter 来实现。

std::cout<<trimline2->ReversedParameter(0.5)<<std::endl;//-0.5

子类

除了 Geom2OffsetCurve 外，其他均与三维类似。

Geom2Line

Geom2Line 是一条无限长的 2D 直线，由一个 Point2 和一个 Direction2 定义，在 Point2 处的参数为 0.0，沿 Direction2 方向参数为正，参数变化与长度变化一致。直线的参数域为无穷大。

auto line = std::make_shared<AMCAX::Geom2Line>(AMCAX::Point2(0., 1.), AMCAX::Direction2(1., 2.));
auto trimline = std::make_shared<AMCAX::Geom2TrimmedCurve>(line, 0.0, 1.0);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge2d(trimline), "trimline.brep");

Geom2Circle

Geom2Circle 是 2 维空间中的圆，由一个标架和半径定义，即在标架的 XOY 平面上的标准圆（圆心在标架原点，参数为 0 时，圆上的点在 x 轴，参数增加时逆时针转动）。圆的参数域为[0, 2*pi)，意义为圆的参数坐标。

auto circle = std::make_shared<AMCAX::Geom2Circle>(AMCAX::Frame2(), 1.0);

AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge2d(circle), "circle.brep");

Geom2Ellipse

Geom2Ellipse 是 2 维空间中的椭圆，由一个标架和长短半径定义，即在标架的 XOY 平面上的标准椭圆（中心在标架原点，参数为 0 时，椭圆上的点在 x 轴，参数增加时逆时针转动）。椭圆的参数域为[0, 2*pi)，意义为椭圆的参数坐标。

auto ellipse = std::make_shared<AMCAX::Geom2Ellipse>(AMCAX::Frame2(), 2.0,1.0);

AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge2d(ellipse), "ellipse.brep");

Geom2Hyperbola

Geom2Hyperbola 是 2 维空间中双曲线的右半支，由一个标架和实轴半径、虚轴半径定义，即在标架的 XOY 平面上的标准双曲线的右半支（中心在标架原点，参数为 0 时，双曲线上的点在 x 轴的正半轴上，参数增加时，点沿着双曲线的右半支移动，并且参数越大，在 XOY 平面上的 y 坐标就越大）。如果想获取双曲线的左半支，可以通过 AMCAX::Geom2Hyperbola::OtherBranch 获得。双曲线的参数域为[-∞, +∞]，意义为双曲线的参数坐标。

auto hyperbola = std::make_shared<AMCAX::Geom2Hyperbola>(AMCAX::Frame2(), 2.0, 1.0);
auto trimhyperbola = std::make_shared<AMCAX::Geom2TrimmedCurve>(hyperbola, 0.0, 2.0);
AMCAX::Hyperbola2 otherbranch= hyperbola->OtherBranch();
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge2d(trimhyperbola), "trimhyperbola.brep");
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge2d(otherbranch,0.0,2.0), "otherbranch.brep");

Geom2Parabola

Geom2Parabola 是 2 维空间中的抛物线，由一个标架和焦距定义，即在标架的 XOY 平面上的标准抛物线（顶点在标架原点，对称轴为 x 轴，参数为 0 时，抛物线上的点在原点，参数增加时，点沿着抛物线移动，并且参数越大，在 XOY 平面上的 y 坐标就越大）。抛物线的参数域为[-∞, +∞]，意义为抛物线的参数坐标。

auto parabola = std::make_shared<AMCAX::Geom2Parabola>(AMCAX::Frame2(), 1.0);
auto trimparabola = std::make_shared<AMCAX::Geom2TrimmedCurve>(hyperbola, -2.0, 2.0);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge2d(trimparabola), "trimparabola.brep");

Geom2BezierCurve

Geom2BezierCurve 是 2 维空间中的 Bezier 曲线，由控制点、权重（可选）定义。曲线的次数为控制点数量减一，例如，如果有 4 个控制点，则曲线是 3 次 Bezier 曲线。另外 Bezier 曲线的参数域为 [0,1]，当参数 t=0 时，曲线位于起点（第一个控制点），当参数 t=1 时，曲线位于终点（最后一个控制点）。对于标准的贝塞尔曲线，其节点向量为 {0, 1}，且每个节点的重数都是次数 + 1。

std::vector<AMCAX::Point2> pts = {
   AMCAX::Point2(0.0, 0.0),
   AMCAX::Point2(2.0, 2.0),
   AMCAX::Point2(4.0, 3.0),
};
auto bezier = std::make_shared<AMCAX::Geom2BezierCurve>(pts);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge2d(bezier), "bezier.brep");

Geom2BSplineCurve

Geom2BSplineCurve 是 2 维空间中的 BSpline 曲线，由控制点、节点、节点重数、曲线次数、权重（可选）定义。

std::vector<AMCAX::Point2> pts2 = {
   AMCAX::Point2(0.5, 0.5),
   AMCAX::Point2(1.0, 3.0),
   AMCAX::Point2(3.0, 1.0),
   AMCAX::Point2(3.8,2.0),
   AMCAX::Point2(2.5,3.5),
   AMCAX::Point2(1.0,0.5),
   AMCAX::Point2(0.3,2.0)
};
std::vector<double> knots2 = { 0.0, 0.25, 0.5,0.75,1.0 };
std::vector<int> mults2 = { 4, 1, 1,1,4 };
auto bspline = std::make_shared< AMCAX::Geom2BSplineCurve>(pts2, knots2, mults2, 3);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge2d(bspline), "bspline.brep");

Geom2TrimmedCurve

Geom2TrimmedCurve 是 2 维空间中的裁剪曲线，由原曲线和两个裁剪参数组成。与 3 维相同，Trim 后的曲线一定是非周期的并且周期曲线可以超过定义域进行裁剪，如对圆：

auto circle = std::make_shared<AMCAX::Geom2Circle>(AMCAX::Frame2(), 1.0);
auto trimcircle2 = std::make_shared<AMCAX::Geom2TrimmedCurve>(circle, -AMCAX::Constants::pi / 4, AMCAX::Constants::pi * 3 / 4);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge2d(trimcircle2), "trimcircle2.brep");

Geom2OffsetCurve

Geom2OffsetCurve 是 2 维空间中的偏移曲线，由原曲线、偏移距离组成，其偏移方向为切向顺时针旋转90°。另外如果想获取偏移曲线的原曲线，可通过 AMCAX::Geom2OffsetCurve::BasisCurve 来获得。

auto circle2 = std::make_shared<AMCAX::Geom2Circle>(AMCAX::Frame2(), 2.0);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge2d(circle2), "circle2.brep");
//Get the 2D offset curve
double offset = 1.5;
auto circleoffset = std::make_shared<AMCAX::Geom2OffsetCurve>(circle2, offset);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge2d(circleoffset), "circleoffset.brep");
//Get the basiscurve
auto basiscircle = circleoffset->BasisCurve();
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge2d(basiscircle), "basis.brep");

三维参数曲线

常见功能

获得参数范围

AMCAX::Geom3Curve::FirstParameter 用于获得曲线的起始参数， AMCAX::Geom3Curve::LastParameter 用于获得曲线的终止参数。

//1
//Make a 3D BSplineCurve
std::vector<AMCAX::Point3> pts22 = {
AMCAX::Point3(0.5, 0.5,0.3),
AMCAX::Point3(1.0, 3.0,0.4),
AMCAX::Point3(3.0, 1.0,0.1),
AMCAX::Point3(3.8,2.0,0.6),
AMCAX::Point3(2.5,3.5,0.8),
AMCAX::Point3(1.0,0.5,0.9),
AMCAX::Point3(0.3,2.0,0.5)
};
std::vector<double> weights = { 1.0, 2.0, 3.0, 4.0, 3.0, 2.0, 1.0 };
std::vector<double> knots = { 0.0, 0.25, 0.5, 1.0 };
std::vector<int> mults = { 4, 1, 2, 4 };
std::shared_ptr< AMCAX::Geom3BSplineCurve> bspline = std::make_shared< AMCAX::Geom3BSplineCurve>(pts22, weights, knots, mults, 3);
//Get the FirstParameter and LastParameter
double fp = bspline->FirstParameter();
double lp = bspline->LastParameter();
std::cout << fp <<"," << lp << std::endl;//0,1
 
//2
//Make a trimcurve
AMCAX::MakeGeom3Parabola p(AMCAX::Frame3(), 2.0);
std::shared_ptr< AMCAX::Geom3Parabola >parabola = p.Value();
AMCAX::Geom3TrimmedCurve trimcurve(parabola, -2.0, 2.0);
//Get the FirstParameter and LastParameter
double fp2 = trimcurve.FirstParameter();
double lp2 = trimcurve.LastParameter();
std::cout << fp2 << "," << lp2 << std::endl;//-2,2

求值和求导

AMCAX::Geom3Curve::Value 或 AMCAX::Geom3Curve::D0 用于求值，而 AMCAX::Geom3Curve::D1 ， AMCAX::Geom3Curve::D2 ， AMCAX::Geom3Curve::D3 ， AMCAX::Geom3Curve::DN 用于求导。

//1
//Value
double t = 0.4 * (fp + lp);
AMCAX::Point3 p1 = bspline->Value(t);
//D0 D1 D2 D3 DN
AMCAX::Point3 p2;
AMCAX::Vector3 d1, d2, d3;
bspline->D0(t, p2);
bspline->D1(t, p2, d1);
bspline->D2(t, p2, d1, d2);
bspline->D3(t, p2, d1, d2, d3);
int deriv = 4;
AMCAX::Vector3 dn = bspline->DN(t, deriv);
 
//2
//Value
double t2 = 1.5;
AMCAX::Point3 p3 = trimcurve.Value(t2);
//D0 D1 D2 D3 DN
AMCAX::Point3 p4;
AMCAX::Vector3 dd1, dd2, dd3;
trimcurve.D0(t2, p4);
trimcurve.D1(t2, p4, dd1);
trimcurve.D2(t2, p4, dd1, dd2);
trimcurve.D3(t2, p4, dd1, dd2, dd3);
int deriv2 = 4;
AMCAX::Vector3 ddn = trimcurve.DN(t2, deriv2);

获得类型

AMCAX::Geom3Curve::Type 用于获得曲线类型，如直线、圆、椭圆、抛物线等。曲线类型可参考枚举类 CurveType 。

std::cout << int(bspline->Type()) << ";" << int(trimcurve.Type());//7;8

封闭性、周期性

AMCAX::Geom3Curve::IsClosed 用于获得曲线的封闭性（起始点与终止点是同一个点）， AMCAX::Geom3Curve::IsPeriodic 用于获得曲线的周期性。

std::cout <<bspline->IsClosed()<< ";" << bspline->IsPeriodic();//0;0

std::cout <<trimcurve.IsClosed()<< ";" << trimcurve.IsPeriodic();//0;0

反向

AMCAX::Geom3Curve::Reverse 用于将 Geom3Curve 反向，改变自身，而 AMCAX::Geom3Curve::Reversed 用于获取反向的 Geom3Curve，不改变自身。反转后，曲线的起点和终点发生了对换。对于一般曲线，曲线参数范围不变，而对于裁剪曲线，可能会改变曲线的参数范围。如以下例子，一条裁剪直线原来的参数范围为 -1 到 3，反转后变为 -3 到 1。

//1
//reversed
auto reverse = bspline->Reversed();
double fp3 = reverse->FirstParameter();
double lp3 = reverse->LastParameter();
std::cout << fp3 << "," << lp3 << std::endl;//0,1
std::cout << bspline->Value(fp) << std::endl;//0.5 0.5 0.3
std::cout << bspline->Value(lp) << std::endl;//0.3 2 0.5
std::cout<<reverse->Value(fp3)<<std::endl;//0.3 2 0.5
std::cout<<reverse->Value(lp3)<<std::endl;//0.5 0.5 0.3
 
//reverse
bspline->Reverse();
double fp4 = bspline->FirstParameter();
double lp4 = bspline->LastParameter();
std::cout << fp4 << "," << lp4 << std::endl;//0,1
std::cout << reverse->Value(fp4) << std::endl;//0.3 2 0.5
std::cout << reverse->Value(lp4) << std::endl;//0.5 0.5 0.3
 
//2
auto line2 = std::make_shared<AMCAX::Geom3Line>(AMCAX::Point3(0., 0., 0.), AMCAX::Direction3(1., 0., 0.));
auto trimline2 = std::make_shared<AMCAX::Geom3TrimmedCurve>(line2, -1.0, 3.0);
std::cout << trimline2->Value(-1.0) << std::endl;//-1 0 0
std::cout << trimline2->Value(3.0) << std::endl;//3 0 0
//reversed
auto reverse2 = trimline2->Reversed();
double fp5 = reverse2->FirstParameter();
double lp5 = reverse2->LastParameter();
std::cout << fp5 << "," << lp5 << std::endl;//-3,1
std::cout << reverse2->Value(fp5) << std::endl;//3 0 0
std::cout << reverse2->Value(lp5) << std::endl;//-1 0 0
 
//reverse
trimline2->Reverse();
double fp6 = trimline2->FirstParameter();
double lp6 = trimline2->LastParameter();
std::cout << fp6 << "," << lp6 << std::endl;//-3,1
std::cout << trimline2->Value(fp6) << std::endl;//3 0 0
std::cout <<trimline2->Value(lp6) << std::endl;//-1 0 0

在这里我们解释一下反转后，裁剪直线的参数范围变为 -3 到 1 的原因，这是因为裁剪曲线在反转的时候是先对其 basiscurve （无穷长的直线）做反转，然后再根据裁剪起始点和终止点的参数确定反转后的参数。

另外如果想计算某一参数的对称参数可通过 AMCAX::Geom3Curve::ReversedParameter 来实现。

std::cout << trimline->ReversedParameter(0.5) << std::endl;//-0.5

子类

Geom3Line

Geom3Line 是一条无限长的 3D 直线，由一个 Point3 和一个 Direction3 定义，在 Point3 处的参数为 0.0，沿 Direction3 方向参数为正，参数变化与长度变化一致。直线的参数域为无穷大。

auto line = std::make_shared<AMCAX::Geom3Line>(AMCAX::Point3(0., 1., 1.), AMCAX::Direction3(1., 2., 3.));
auto trimline = std::make_shared<AMCAX::Geom3TrimmedCurve>(line, 0.0, 1.0);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge(trimline), "trimline.brep");

Geom3Circle

Geom3Circle 是 3 维空间中的圆，由一个标架和半径定义，即在标架的 XOY 平面上的标准圆（圆心在标架原点，参数为 0 时，圆上的点在 x 轴，参数增加时逆时针转动）。圆的参数域为[0, 2*pi)，意义为圆的参数坐标。

auto circle = std::make_shared<AMCAX::Geom3Circle>(AMCAX::Frame3(), 1.0);

AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge(circle), "circle.brep");

Geom3Ellipse

Geom3Ellipse 是 3 维空间中的椭圆，由一个标架和长短半径定义，即在标架的 XOY 平面上的标准椭圆（中心在标架原点，参数为 0 时，椭圆上的点在 x 轴，参数增加时逆时针转动）。椭圆的参数域为[0, 2*pi)，意义为椭圆的参数坐标。

auto ellipse = std::make_shared<AMCAX::Geom3Ellipse>(AMCAX::Frame3(), 2.0,1.0);

AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge(ellipse), "ellipse.brep");

Geom3Hyperbola

Geom3Hyperbola 是 3 维空间中双曲线的右半支，由一个标架和实轴半径、虚轴半径定义，即在标架的 XOY 平面上的标准双曲线的右半支（中心在标架原点，参数为 0 时，双曲线上的点在 x 轴的正半轴上，参数增加时，点沿着双曲线的右半支移动，并且参数越大，在 XOY 平面上的 y 坐标就越大）。如果想获取双曲线的左半支，可以通过 AMCAX::Geom3Hyperbola::OtherBranch 获得。双曲线的参数域为[-∞, +∞]，意义为双曲线的参数坐标。

auto hyperbola = std::make_shared<AMCAX::Geom3Hyperbola>(AMCAX::Frame3(), 2.0, 1.0);
auto trimhyperbola = std::make_shared<AMCAX::Geom3TrimmedCurve>(hyperbola, 0.0, 2.0);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge(trimhyperbola), "trimhyperbola.brep");

Geom3Parabola

Geom3Parabola 是 3 维空间中的抛物线，由一个标架和焦距定义，即在标架的 XOY 平面上的标准抛物线（顶点在标架原点，对称轴为 x 轴，参数为 0 时，抛物线上的点在原点，参数增加时，点沿着抛物线移动，并且参数越大，在 XOY 平面上的 y 坐标就越大）。抛物线的参数域为[-∞, +∞]，意义为抛物线的参数坐标。

auto parabola2 = std::make_shared<AMCAX::Geom3Parabola>(AMCAX::Frame3(), 1.0);
auto trimparabola = std::make_shared<AMCAX::Geom3TrimmedCurve>(parabola2, -2.0, 2.0);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge(trimparabola), "trimparabola.brep");

Geom3BezierCurve

Geom3BezierCurve 是 3 维空间中的 Bezier 曲线，由控制点、权重（可选）定义。曲线的次数为控制点数量减一，例如，如果有 4 个控制点，则曲线是 3 次 Bezier 曲线。另外 Bezier 曲线的参数域为 [0,1]，当参数 t=0 时，曲线位于起点（第一个控制点），当参数 t=1 时，曲线位于终点（最后一个控制点）。对于标准的贝塞尔曲线，其节点向量为 {0, 1}，且每个节点的重数都是次数 + 1。

std::vector<AMCAX::Point3> pts3 = {
AMCAX::Point3(0.0, 0.0,0.0),
AMCAX::Point3(2.0, 2.0,2.0),
AMCAX::Point3(4.0, 3.0,5.0),
AMCAX::Point3(6.0,2.0,4.0)
};
auto bezier = std::make_shared<AMCAX::Geom3BezierCurve>(pts3);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge(bezier), "bezier.brep");

Geom3BSplineCurve

Geom3BSplineCurve 是 3 维空间中的 BSpline 曲线，由控制点、节点向量、节点重数、权重（可选）定义。

std::vector<AMCAX::Point3> pts = {
AMCAX::Point3(0.5, 0.5,0.3),
AMCAX::Point3(1.0, 3.0,0.4),
AMCAX::Point3(3.0, 1.0,0.1),
AMCAX::Point3(3.8,2.0,0.6),
AMCAX::Point3(2.5,3.5,0.8),
AMCAX::Point3(1.0,0.5,0.9),
AMCAX::Point3(0.3,2.0,0.5)
};
std::vector<double> weights2 = { 1.0, 2.0, 3.0, 4.0, 3.0, 2.0, 1.0 };
std::vector<double> knots2 = { 0.0, 0.25, 0.5, 1.0 };
std::vector<int> mults2 = { 4, 1, 2, 4 };
auto bspline2 = std::make_shared< AMCAX::Geom3BSplineCurve>(pts, weights2, knots2, mults2, 3);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge(bspline2), "bspline.brep");

Geom3TrimmedCurve

Geom3TrimmedCurve 是 3 维空间中的裁剪曲线，由原曲线和两个裁剪参数组成。要注意的是，Trim 后的曲线一定是非周期的，即使对圆做的是 [0,2pi] 的裁剪。此外，周期曲线可以超过定义域进行裁剪，如对圆：

auto circle = std::make_shared<AMCAX::Geom3Circle>(AMCAX::Frame3(), 1.0);
auto trimcircle2 = std::make_shared<AMCAX::Geom3TrimmedCurve>(circle, -AMCAX::Constants::pi / 4, AMCAX::Constants::pi * 3 / 4);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge(trimcircle2), "trimcircle2.brep");

Geom3OffsetCurve

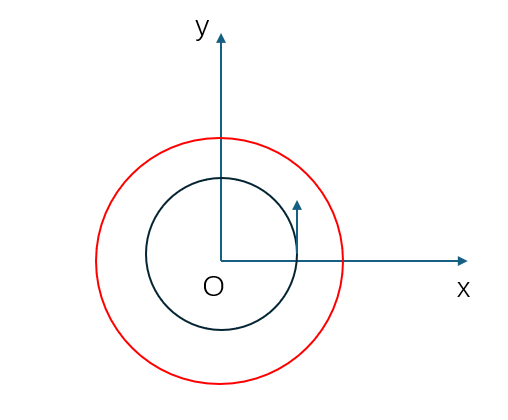
Geom3OffsetCurve 是 3 维空间中的偏移曲线，由原曲线、偏移距离和参考方向组成。其作用为：将原曲线沿垂直于切向的一个方向偏移指定距离，偏移方向为切向和参考方向的外积方向，如下图所示。其中，蓝色箭头为切向，绿色箭头为参考方向，红色箭头为外积方向，即偏移方向。

以 xoy 平面的标准圆为例，当参考方向为 oz 时，偏移方向为向外。以下为偏移后的结果：

另外如果想获取偏移曲线的原曲线，可通过 AMCAX::Geom3OffsetCurve::BasisCurve 来获得。

auto circle2 = std::make_shared<AMCAX::Geom3Circle>(AMCAX::Frame3(), 2.0);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge(circle2), "circle2.brep");
//Get the 3D offset curve
double offset = 1.5;
AMCAX::Direction3 direction(0.0, 0.0, 1.0);
auto circleoffset = std::make_shared<AMCAX::Geom3OffsetCurve>(circle2, offset, direction);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge(circleoffset), "circleoffset.brep");
//Get the basiscurve
auto basiscircle = circleoffset->BasisCurve();

三维参数曲面

常用功能

获得参数范围

Bounds() 获得全部参数，FirstUParameter() 获得起始 u 参数，LastUParameter() 获得结束 u 参数，FirstVParameter() 获得起始 v 参数，LastVParameter() 获得结束 v 参数。

AMCAX::Geom3CylindricalSurface CylindricalSurface4(AMCAX::Frame3(), 2.0);
//Get the parameter bounds
double u1=0., u2=0., v1=0., v2=0.;
CylindricalSurface4.Bounds(u1, u2, v1, v2);
std::cout << u1 << "-" << u2 << std::endl;//0-6.28319
std::cout << v1 << "-" << v2 << std::endl;//-1e+100-1e+100
//Get the FirstUParameter,LastUParameter,FirstVParameter,LastVParameter
std::cout<<CylindricalSurface4.FirstUParameter()<<std::endl;//0
std::cout<<CylindricalSurface4.LastUParameter()<<std::endl;//6.28319
std::cout<<CylindricalSurface4.FirstVParameter()<<std::endl;//-1e+100
std::cout<<CylindricalSurface4.LastVParameter()<<std::endl;//1e+100

求值、求导

Value 或 D0 可以求值，D1，D2，D3，DN 可以求导。

AMCAX::Geom3CylindricalSurface CylindricalSurface4(AMCAX::Frame3(), 2.0);
//value D0 
std::cout << CylindricalSurface4.Value(1., 2.) << std::endl;//1.0806 1.68294 2
AMCAX::Point3 p1;
CylindricalSurface4.D0(1., 2., p1);
std::cout << p1 << std::endl;//1.0806 1.68294 2
//D1
AMCAX::Point3 p2;
AMCAX::Vector3 du1;
AMCAX::Vector3 dv1;
CylindricalSurface4.D1(1., 2., p2, du1, dv1);
std::cout << p2 << std::endl;//1.0806 1.68294 2
std::cout << du1 << std::endl;//-1.68294 1.0806 0
std::cout << dv1 << std::endl;//0 0 1
//D2
AMCAX::Point3 p3;
AMCAX::Vector3 du2;
AMCAX::Vector3 dv2;
AMCAX::Vector3 duu1;
AMCAX::Vector3 duv1;
AMCAX::Vector3 dvv1;
CylindricalSurface4.D2(1., 2., p3, du2, dv2,duu1,duv1,dvv1);
std::cout << p3 << std::endl;//1.0806 1.68294 2
std::cout << du2 << std::endl;//-1.68294 1.0806 0
std::cout << dv2 << std::endl;//0 0 1
std::cout << duu1 << std::endl;//-1.0806 -1.68294 -0
std::cout << duv1 << std::endl;//0 0 0
std::cout << dvv1 << std::endl;//0 0 0
//D3
AMCAX::Point3 p4;
AMCAX::Vector3 du3;
AMCAX::Vector3 dv3;
AMCAX::Vector3 duu2;
AMCAX::Vector3 duv2;
AMCAX::Vector3 dvv2;
AMCAX::Vector3 duuu;
AMCAX::Vector3 duuv;
AMCAX::Vector3 duvv;
AMCAX::Vector3 dvvv;
CylindricalSurface4.D3(1., 2., p4, du3, dv3, duu2, duv2, dvv2,duuu,duuv,duvv,dvvv);
std::cout << p4 << std::endl;//1.0806 1.68294 2
std::cout << du3 << std::endl;//-1.68294 1.0806 0
std::cout << dv3 << std::endl;//0 0 1
std::cout << duu2 << std::endl;//-1.0806 -1.68294 -0
std::cout << duv2 << std::endl;//0 0 0
std::cout << dvv2 << std::endl;//0 0 0
std::cout << duuu << std::endl;//1.98294 -1.0806 0
std::cout << duuv << std::endl;//0 0 0
std::cout << duvv << std::endl;//0 0 0
std::cout << dvvv << std::endl;//0 0 0
//DN
int nu = 4, nv = 4;
std::cout << CylindricalSurface4.DN(1., 2., nu, nv) << std::endl;//0 0 0

获得类型

Type() 可以获得类型，如平面、球等。

std::cout << int(CylindricalSurface4.Type()) << std::endl;//2

封闭性、周期性

IsUClosed() 获得 u 方向的封闭性，IsUPeriodic() 获得 u 方向的周期性，IsVClosed() 获得 v 方向的封闭性，IsVPeriodic() 获得 v 方向的周期性。

std::cout << CylindricalSurface4.IsUClosed() << std::endl;//1
std::cout << CylindricalSurface4.IsUPeriodic() << std::endl;//1
std::cout << CylindricalSurface4.IsVClosed() << std::endl;//0
std::cout << CylindricalSurface4.IsVPeriodic() << std::endl;//0

反向

UReverse() 可以将 u 方向反向，VReverse() 可以将 v 方向反向。需要注意的是，反向后 u 方向和 v 方向的起始和结束参数不会改变，仅是坐标上发生改变。

std::cout << CylindricalSurface4.Value(CylindricalSurface4.FirstUParameter(), CylindricalSurface4.FirstVParameter()) << std::endl;// 2 0 -1e+100
std::cout << CylindricalSurface4.Value(CylindricalSurface4.LastUParameter(), CylindricalSurface4.LastVParameter()) << std::endl;//2 -4.89859e
CylindricalSurface4.UReverse();
CylindricalSurface4.VReverse();
std::cout << CylindricalSurface4.Value(CylindricalSurface4.FirstUParameter(), CylindricalSurface4.FirstVParameter()) << std::endl;//2 0 1e+100
std::cout << CylindricalSurface4.Value(CylindricalSurface4.LastUParameter(), CylindricalSurface4.LastVParameter()) << std::endl;//2 4.89859e-16 -1e+100

另外 UReversedParameter(t) 计算参数 t 在 u 方向上的对称参数，VReversedParameter(t) 计算参数 t 在 v 方向上的对称参数。

std::cout << CylindricalSurface4.UReversedParameter(2.) << std::endl;//4.28319

std::cout << CylindricalSurface4.VReversedParameter(2.) << std::endl;//-2

等参线

UIso() 可以获得 u 等参线，即参数域上直线 u=u0 对应的空间曲线，VIso() 可以获得 v 等参线，即参数域上直线 v=v0 对应的空间曲线。

std::shared_ptr< AMCAX::Geom3Curve >uiso = CylindricalSurface4.UIso(2.);

std::shared_ptr< AMCAX::Geom3Curve >viso = CylindricalSurface4.VIso(2.);

对于上面这个示例，UIso 是一个平行于 Z 轴的直线，位于圆柱的侧面，VIso 是一个半径为 r=2.0 的圆，位于高度 v=2.0 处。

子类

Geom3Plane

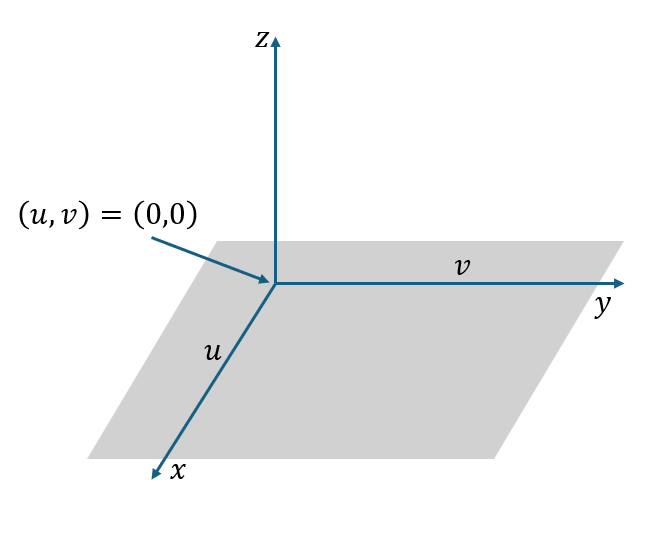
Geom3Plane 是 3 维空间中的平面，其参数域为无穷大。平面可根据 AMCAX::Frame3 创建，Frame3 的 XOY 为平面，OZ 为平面法向。参数域 u 方向即 OX 方向，v 方向即 OY 方向，在 (u, v) = (0, 0) 处的三维空间点为 Frame3 的标架原点。

AMCAX::Frame3 frame;
AMCAX::Geom3Plane plane(frame);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeFace(plane.GetPlane(), 0., 2., 0., 2.), "plane.brep");

Geom3SphericalSurface

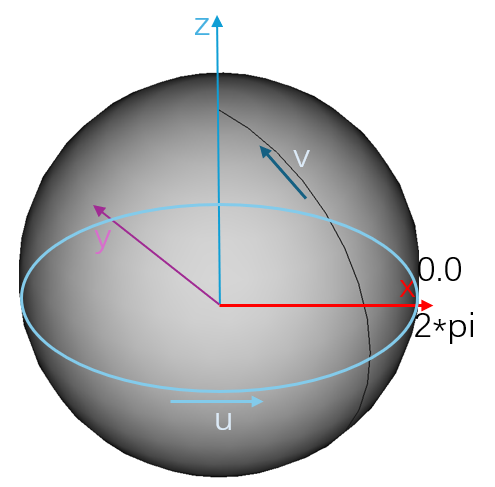
Geom3SphericalSurface 是 3 维空间中的球面，其参数域为 [0, 2pi) x [-pi/2, pi/2]，参数意义为球的参数坐标。圆面可根据 AMCAX::Frame3 和半径创建。Frame3 的原点为球心，XOY 平面上的圆为等参线 v=0，x 正半轴和 z 轴张成的半平面上的半圆为等参线 u=0，ox 向 oy 旋转为 u 方向正向，-oz 向 oz 旋转为 v 方向正向。

AMCAX::Geom3SphericalSurface SphericalSurface(AMCAX::Frame3(), 2.0);

AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeFace(SphericalSurface.GetSphere(), 0., 1., 0., 1.), "SphericalSurface.brep");

AMCAX::Geom3SphericalSurface

三维球面的类

定义 Geom3SphericalSurface.hpp:14

Geom3CylindricalSurface

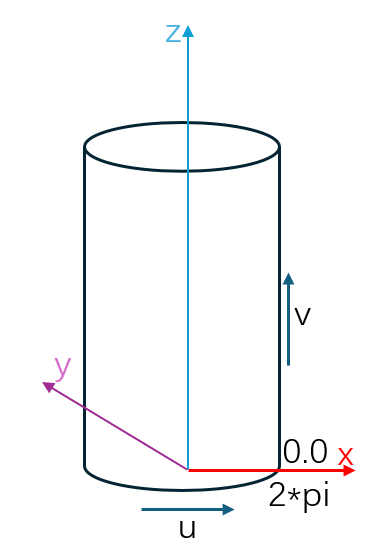
Geom3CylindricalSurface 是 3 维空间中的圆柱面（无限长），其参数域为 [0, 2pi) x [-∞, ∞]，参数意义为圆柱的参数坐标。圆柱面可根据 AMCAX::Frame3 和半径创建，xoy 平面上的圆为等参线 v=0，ox 向 oy 旋转为 u 方向正向，z 方向为 v 方向正向，v 方向的改变与弧长的改变一致。

AMCAX::Geom3CylindricalSurface CylindricalSurface(AMCAX::Frame3(), 2.0);

AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeFace(CylindricalSurface.GetCylinder(), 0., 2., 0., 2.), "CylindricalSurface.brep");

Geom3ConicalSurface

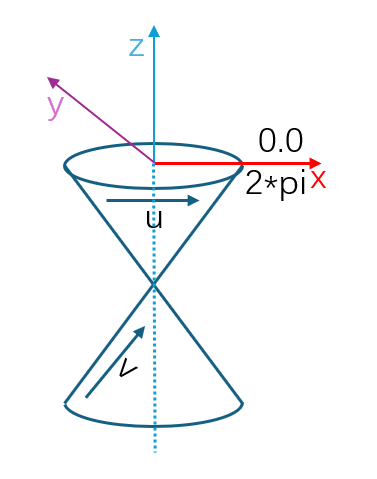
Geom3ConicalSurface 是 3 维空间中的圆锥面（无限长），其参数域为[0, 2pi) x [-∞, ∞]。圆锥面可根据 Frame3、xoy 平面圆的半径和半角创建，xoy 平面上的圆为等参线 v=0，ox 向 oy 旋转为 u 方向正向，v 方向为倾斜的直线，与 z 方向夹角为锐角的方向为正向，v 方向的改变与弧长的改变一致。

AMCAX::Geom3ConicalSurface ConicalSurface(AMCAX::Frame3(), 2.0, 45.0 * AMCAX::Constants::pi / 180.0);

AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeFace(ConicalSurface.GetCone(), 0., 2., 0., 2.), "ConicalSurface.brep");

AMCAX::Geom3ConicalSurface

三维圆锥曲面的类

定义 Geom3ConicalSurface.hpp:14

Geom3ToroidalSurface

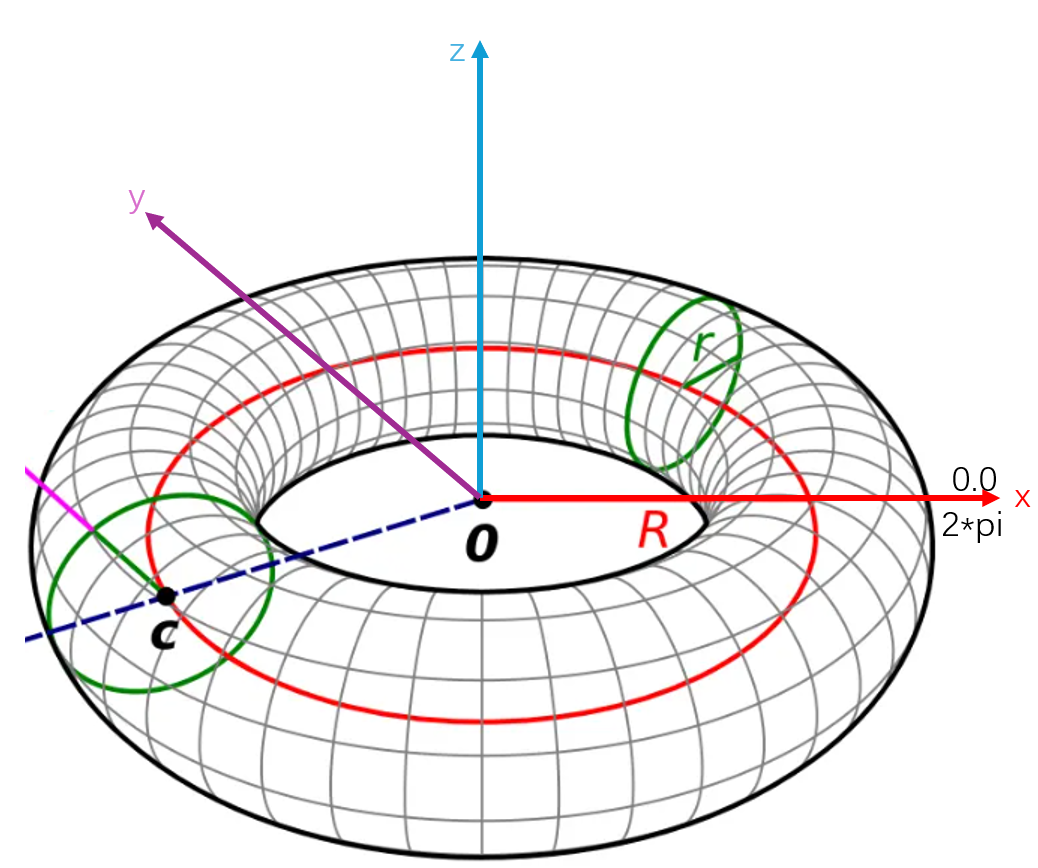
Geom3ToroidalSurface 是 3 维空间中的圆环面，其参数域为 [0, 2pi) x [0, 2pi)。圆环面可根据由 Frame3、大半径和小半径创建。xoy 平面上的标准圆为等参线 v=0，xoz 平面上的标准圆为等参线 u=0。

AMCAX::Geom3ToroidalSurface ToroidalSurface(AMCAX::Frame3(), 2.0, 1.0);

AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeFace(ToroidalSurface.GetTorus(), 0., 2., 0., 2.), "ToroidalSurface.brep");

AMCAX::Geom3ToroidalSurface

三维环形曲面的类

定义 Geom3ToroidalSurface.hpp:14

Geom3BezierSurface

Geom3BezierSurface 是 3 维空间中的 Bezier 曲面，其参数域为 [0,1]x[0,1]。Bezier 曲面可根据控制点、权重（可选）创建，在创建时，需要注意权重的数量必须与控制点的数量一致，如果所有权重相等（例如都为 1），则有理贝塞尔曲面退化为普通贝塞尔曲面。

AMCAX::Array2<AMCAX::Point3> poles(4, 4);
poles(0, 0).SetCoord(0.0, 0.0, 0.0);
poles(0, 1).SetCoord(1.0, 0.0, 2.0);
poles(0, 2).SetCoord(2.0, 0.0, 1.0);
poles(0, 3).SetCoord(3.0, 0.0, 0.0);
poles(1, 0).SetCoord(0.0, 1.0, 1.0);
poles(1, 1).SetCoord(1.0, 1.0, 3.0);
poles(1, 2).SetCoord(2.0, 1.0, 2.0);
poles(1, 3).SetCoord(3.0, 1.0, 1.0);
poles(2, 0).SetCoord(0.0, 2.0, 1.0);
poles(2, 1).SetCoord(1.0, 2.0, 2.0);
poles(2, 2).SetCoord(2.0, 2.0, 3.0);
poles(2, 3).SetCoord(3.0, 2.0, 1.0);
poles(3, 0).SetCoord(0.0, 3.0, 0.0);
poles(3, 1).SetCoord(1.0, 3.0, 1.0);
poles(3, 2).SetCoord(2.0, 3.0, 1.0);
poles(3, 3).SetCoord(3.0, 3.0, 0.0);
 
AMCAX::Array2<double> weights(4, 4);
for (int i = 0; i < 4; ++i) {
    for (int j = 0; j < 4; ++j) {
        weights(i, j) = 1.0;
    }
}
 
std::shared_ptr<AMCAX::Geom3BezierSurface> BezierSurface = std::make_shared<AMCAX::Geom3BezierSurface>(poles, weights);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeFace(BezierSurface, AMCAX::Precision::Confusion()), "BezierSurface.brep");

Geom3BSplineSurface

Geom3BSplineSurface 是 3 维空间中的 BSpline 曲面，BSpline 曲面可根据控制点、节点向量、节点重数、曲线次数创建。在创建时，需要满足以下条件：UKnots 的长度 = UMultiplicities 的长度；VKnots 的长度 = VMultiplicities 的长度；sum(UMultiplicities) = Poles.Rows() + UDegree + 1；sum(VMultiplicities) = Poles.Cols() + VDegree + 1；节点向量必须是单调递增的，且每个节点的重数不能超过曲线的次数。

AMCAX::Array2<AMCAX::Point3> poles2(4, 4);
poles2(0, 0).SetCoord(0.0, 0.0, 0.0);
poles2(0, 1).SetCoord(0.666667, 1., 0.333333);
poles2(0, 2).SetCoord(-0.666667, 0., -0.333333);
poles2(0, 3).SetCoord(0.0, 1., 0.0);
poles2(1, 0).SetCoord(0.666667, 1., 0.333333);
poles2(1, 1).SetCoord(1.44444, 2.22222, 0.777778);
poles2(1, 2).SetCoord(-1.22222, 1.22222, 0.111111);
poles2(1, 3).SetCoord(-0.666667, 2., 0.333333);
poles2(2, 0).SetCoord(0.333333, 1., -0.333333);
poles2(2, 1).SetCoord(1.11111, 0.222222, 0.111111);
poles2(2, 2).SetCoord(2.44444, 3.22222, 0.777778);
poles2(2, 3).SetCoord(1.66667, 2., 0.333333);
poles2(3, 0).SetCoord(1., 0.0, 0.0);
poles2(3, 1).SetCoord(1.66667, -1., 0.333333);
poles2(3, 2).SetCoord(1.66667, 2., 0.333333);
poles2(3, 3).SetCoord(1., 1., 0.);
std::vector<double> uknots = { 0.0, 1.0 };
std::vector<int> umults = { 4, 4 };
std::vector<double> vknots = { 0.0, 1.0 };
std::vector<int> vmults = { 4, 4 };
std::shared_ptr<AMCAX::Geom3BSplineSurface> BSplineSurface = std::make_shared<AMCAX::Geom3BSplineSurface>(poles2, uknots, vknots, umults, vmults, 3, 3);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeFace(BSplineSurface, AMCAX::Precision::Confusion()), "BSplineSurface.brep");

Geom3SurfaceOfExtrusion

Geom3SurfaceOfExtrusion 是 3 维空间中的挤出面（拉伸面）（无限大），挤出面可根据母线（Geom3Curve）和挤出方向创建，u 方向为母线的参数方向，v 方向为挤出反向，等参线 v=0 为母线，任一 u 等参线为直线。u 参数域为母线参数域，v 参数域为无穷。

std::shared_ptr<AMCAX::Geom3Curve> curve = std::make_shared<AMCAX::Geom3Circle>(AMCAX::Frame3(), 1.0);
std::shared_ptr<AMCAX::Geom3SurfaceOfExtrusion> SurfaceOfExtrusion = std::make_shared<AMCAX::Geom3SurfaceOfExtrusion>(curve, AMCAX::Direction3(0.0, 0.0, 1.0));
std::shared_ptr<AMCAX::Geom3TrimmedSurface> trimex = std::make_shared<AMCAX::Geom3TrimmedSurface>(SurfaceOfExtrusion, 0., 2*AMCAX::Constants::pi, 0., 5.);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeFace(trimex, AMCAX::Precision::Confusion()), "SurfaceOfExtrusion.brep");

Geom3SurfaceOfRevolution

Geom3SurfaceOfRevolution 是 3 维空间中的旋转面，旋转面可根据母线（Geom3Curve）和旋转轴创建，u 参数域为 [0, 2pi)，v 参数域为母线参数域，每条 v 等参线是一个圆心在旋转轴上的圆，每条 u 等参线可以由母线绕轴旋转得到。

AMCAX::Point3 p;
AMCAX::Direction3 dir(1.0, 0.0, 0.0);
std::shared_ptr<AMCAX::Geom3Curve> curve2 = std::make_shared<AMCAX::Geom3Circle>(AMCAX::Frame3(), 1.0);
std::shared_ptr<AMCAX::Geom3TrimmedCurve> trimCurve = std::make_shared<AMCAX::Geom3TrimmedCurve>(curve2, 0.0, AMCAX::Constants::pi/4);
 
AMCAX::Axis3 axis(p, dir);
std::shared_ptr<AMCAX::Geom3SurfaceOfRevolution> SurfaceOfRevolution = std::make_shared<AMCAX::Geom3SurfaceOfRevolution>(trimCurve, axis);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeFace(SurfaceOfRevolution, AMCAX::Precision::Confusion()), "SurfaceOfRevolution.brep");

Geom3TrimmedSurface

Geom3TrimmedSurface 是 3 维空间中的裁剪曲面，由原曲面和裁剪参数构建。可以在 u 方向裁剪、v 方向裁剪或 uv 方向一起裁剪原曲面。如果想获取原曲面可通过 AMCAX::Geom3TrimmedSurface::BasisSurface 来实现。

std::shared_ptr<AMCAX::Geom3CylindricalSurface> CylindricalSurface2= std::make_shared< AMCAX::Geom3CylindricalSurface>(AMCAX::Frame3(), 3.0);
std::shared_ptr<AMCAX::Geom3TrimmedSurface> TrimmedSurface = std::make_shared<AMCAX::Geom3TrimmedSurface>(CylindricalSurface2, 0., 5., false);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeFace(TrimmedSurface, AMCAX::Precision::Confusion()), "TrimmedSurface.brep");
//Get the basissurface
auto basis = TrimmedSurface->BasisSurface();

Geom3OffsetSurface

Geom3OffsetSurface 是 3 维空间中的偏移曲面，其用于将原曲面的每个点沿法向偏移一定距离。如果想获取原曲面可通过 AMCAX::Geom3OffsetSurface::BasisSurface 来实现。

std::shared_ptr<AMCAX::Geom3CylindricalSurface> CylindricalSurface3 = std::make_shared< AMCAX::Geom3CylindricalSurface>(AMCAX::Frame3(), 2.0);
std::shared_ptr<AMCAX::Geom3TrimmedSurface> TrimmedSurface2 = std::make_shared<AMCAX::Geom3TrimmedSurface>(CylindricalSurface3, 0., 5., false);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeFace(TrimmedSurface2, AMCAX::Precision::Confusion()), "TrimmedSurface2.brep");
//Get the 3D offset surface
std::shared_ptr<AMCAX::Geom3OffsetSurface> offsetsurface1 = std::make_shared<AMCAX::Geom3OffsetSurface>(TrimmedSurface2, 2.);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeFace(offsetsurface1, AMCAX::Precision::Confusion()), "offsetsurface1.brep");
//Get the basissurface
auto basis2 = offsetsurface1->BasisSurface();
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeFace(basis2, AMCAX::Precision::Confusion()), "basis.brep");

如果想获取偏移后的等价曲面可通过 AMCAX::Geom3OffsetSurface::Surface 来实现，如球偏移后还是球，圆柱偏移后还是圆柱。

AMCAX::Geom3OffsetSurface offs(TrimmedSurface2, 2.);
std::shared_ptr<AMCAX::Geom3Surface> offsetsurface2 = offs.Surface();
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeFace(offsetsurface2, AMCAX::Precision::Confusion()), "offsetsurface2.brep");

事实上，上述所有类型偏移后的曲面（平面、球、圆柱、圆锥、圆环、挤出面、旋转面、Bezier、BSpline ）都可以用原曲面类型表示，但仅实现了裁剪或非裁剪的平面、圆柱、圆锥、球、圆环的等价曲面，其余会返回空指针。