坐标

构建

使用默认构造函数会得到坐标原点，构建时需要输入浮点数。另外所有的几何都只支持输入浮点数，后续不再特殊说明。

Coord3（三维坐标）

AMCAX::Coord3 crd1(0.0, 0.0, 2.0);

AMCAX::Coord3

Coord3d Coord3

三维坐标

定义 CoordT.hpp:2810

Coord2（二维坐标）

AMCAX::Coord2 crd2d(0.0,1.0);

AMCAX::Coord2

Coord2d Coord2

二维坐标

定义 CoordT.hpp:2807

获取与更改

获取

获取坐标某一维度的值可以使用如下两种方法。

AMCAX::Coord3 crd(0.0, 1.0, 2.0);
//Method 1
double x = crd.X();
double y = crd.Y();
double z = crd.Z();
//Method 2
double x2 = crd[0];
double y2 = crd[1];
double z2 = crd[2];

更改

更改坐标某一维度的值可以使用如下方法。

AMCAX::Coord3 crd(0.0, 1.0, 2.0);
 
crd.SetX(0.5);
crd.SetY(0.5);
crd.SetZ(0.5);

常用功能

运算

支持加减，数乘，内积，外积，另外也支持 == 和 !=。

加减

AMCAX::Coord3 crd1(2.0, 1.0, 2.0);
AMCAX::Coord3 crd2(0.2, 1.0, 1.0);
//+
AMCAX::Coord3 crd3 = crd1 + crd2;
//-
AMCAX::Coord3 crd4 = crd1 - crd2;

数乘

AMCAX::Coord3 crd5 = crd1 * 0.5;

内积

double t = crd1.Dot(crd2);

外积

AMCAX::Coord3 crd6 = crd1.Cross(crd2);

== 和 !=

== 和 != 可用来对坐标/坐标各维度进行判断。

double result1 = crd1 == crd2;
std::cout << result1 << std::endl;
double result2 = crd1 != crd2;
std::cout << result2 << std::endl;
double result3 = crd1.Y() == crd2.Y();
std::cout << result3 << std::endl;

模

我们内核支持计算坐标的模长以及对坐标进行归一化。

模长

double length = crd1.Norm();

归一化

对坐标进行归一化有两种方式，一种不改变坐标本身，创建一个新的坐标，另一种则是直接改变坐标本身。

AMCAX::Coord3 crd2 = crd.Normalized();
 
//change
crd.Normalize();

输出与输入

我们内核支持对坐标进行输出<<，也支持输入>>。

输出

std::cout << crd1 << std::endl;

输入

AMCAX::Coord3 crd7;
std::istringstream is("0.0 1.0 2.0");
is >> crd7;

点

构建

使用默认构造函数会得到原点。可直接创建或者基于 Coord3/Coord2 构建。

Coord3（三维点）

//Method 1
AMCAX::Point3 p1(0.0, 1.0, 2.0);
//Method 2
AMCAX::Coord3 crd1(0.0, 1.0, 2.0);
AMCAX::Point3 p2(crd1);

Coord2（二维点）

//Method 1
AMCAX::Point2 p3(0.0, 1.0);
//Method 2
AMCAX::Coord2 crd2(0.0, 1.0);
AMCAX::Point2 p4(crd2);

获取与更改

获取

获取点某一维度的值可以使用如下两种方法。

AMCAX::Point3 p1(0.0, 1.0, 2.0);
//Method 1
double x = p1.X();
double y = p1.Y();
double z = p1.Z();
//Method 2
double x2 = p1[0];
double y2 = p2[1];
double z2 = p3[2];

更改

更改点某一维度的值可以使用如下两种方法。

AMCAX::Point3 p1(0.0, 1.0, 2.0);
//Method 1
p1.SetCoord(1.0, 0.0, 2.1);
//Method 2
p1.SetX(0.5);
p1.SetY(0.5);
p1.SetZ(0.5);

常用功能

运算

我们内核不支持对点做四则运算（加减乘除），事实上除 Coord 外，大部分几何都不支持四则运算，后续不再说明。但是如果需要对点做四则运算，可先获取点的 Coord ，然后再对 Coord 做运算。

AMCAX::Point3 p1(0.0, 1.0, 2.0);
AMCAX::Point3 p2(1.0, 2.0, 2.0);
const Coord3& crd3 = p1.Coord();
const Coord3& crd4 = p2.Coord();
const Coord3& crd5 = crd3 + crd4;
AMCAX::Point3 p3(crd5);

计算两点间的距离

AMCAX::Point3 p1(0.0, 1.0, 2.0);
AMCAX::Point3 p2(1.0, 2.0, 2.0);
double dis = p1.Distance(p2);

向量与方向

Vector3 即数学上的向量，有方向有长度。Direction3 只有方向，其模长必须为 1.0。

构建

//Default
AMCAX::Vector3 vec; // (0.0,0.0,0.0)
AMCAX::Direction3 dir; // (1.0, 0.0, 0.0)
std::cout << vec << ' ' << dir << std::endl;
//1
AMCAX::Vector3 vec1(0.1, 2.0, -3.3);
AMCAX::Direction3 dir1(0.1, 2.0, -3.3); // automatically normalized
std::cout << vec1 << ' ' << dir1 << std::endl;
//2
AMCAX::Vector3 vec2(dir1);
AMCAX::Direction3 dir2(vec1);
std::cout << vec2 << ' ' << dir2 << std::endl;
//3
AMCAX::Point3 p1(0.0, 0.0, 0.0);
AMCAX::Point3 p2(1.0, 0.0, 0.0);
AMCAX::Vector3 vec3(p1, p2); // build vector P1P2
std::cout << vec3 << std::endl;

获取与更改

与 Coord 类似，只不过 Direction 会自动归一化。

获取

获取向量/方向某一维度的值可以使用如下两种方法。

AMCAX::Vector3 vec; // (0.0,0.0,0.0)
AMCAX::Direction3 dir; // (1.0, 0.0, 0.0)
//vector
//Method 1
double x = vec.X();
double y = vec.Y();
double z = vec.Z();
//Method 2
double x2 = vec[0];
double y2 = vec[1];
double z2 = vec[2];
 
//direction
//Method 1
double x3 = dir.X();
double y3 = dir.Y();
double z3 = dir.Z();
//Method 2
double x4 = dir[0];
double y4 = dir[1];
double z4 = dir[2];

更改

更改向量/方向某一维度的值可以使用如下两种方法。

//vector
//Method 1
vec.SetCoord(0.1, 2.0, -3.3);
//Method 2
vec.SetX(0.1);
vec.SetY(2.0);
vec.SetZ(-3.3);
 
//direction
//Method 1
dir.SetCoord(0.1, 2.0, -3.3);
//Method 2
dir.SetX(0.1);
dir.SetY(2.0);
dir.SetZ(-3.3);

常用功能

运算

Vector 有加减、数乘，对应数学上的向量加减和数乘，Direction 没有。而内积、外积两者都是有的。用法与 Coord 类似。

加减

AMCAX::Vector3 vec1(0.1, 2.0, -3.3);
AMCAX::Vector3 vecc(2.1, 1.5, 2.3);
//+
AMCAX::Vector3 vecc1 = vecc + vec1;
//-
AMCAX::Vector3 vecc2 = vecc - vec1;

数乘

AMCAX::Vector3 vecc(2.1, 1.5, 2.3);

AMCAX::Vector3 vecc3 = vecc * 2.0;

内积

//vector
AMCAX::Vector3 vec1(0.1, 2.0, -3.3);
AMCAX::Vector3 vecc(2.1, 1.5, 2.3);
double t = vecc.Dot(vec1);
 
//direction
AMCAX::Direction3 dir1(0.1, 2.0, -3.3);
AMCAX::Direction3 dirr(2.3, 1.6, 1.3);
double t2 = dirr.Dot(dir1);

外积

//vector
AMCAX::Vector3 vec1(0.1, 2.0, -3.3);
AMCAX::Vector3 vecc(2.1, 1.5, 2.3);
AMCAX::Vector3 vecc4 = vecc.Cross(vec1);
 
//direction
AMCAX::Direction3 dir1(0.1, 2.0, -3.3);
AMCAX::Direction3 dirr(2.3, 1.6, 1.3);
AMCAX::Direction3 dirr2 = dirr.Cross(dir1);

角度

内核支持计算角度，其中 Angle() 计算的是夹角，角度范围为 [0.0, pi]；AngleWithRef() 计算的是 2d 上的转角，角度范围为 [-pi, pi]，正负值取决于 ddir, other_dir, ref_dir 构成的是右手系还是左手系。

AMCAX::Direction3 ddir(1.0, 0.0, 0.0), other_dir(0.0, 0.5, 0.5), ref_dir(0.0, 0.0, 1.0);
double angle1 = ddir.Angle(other_dir);
double angle2 = ddir.AngleWithRef(other_dir, ref_dir);

注：在二维情况下只可以用 Angle() 来计算转角。
此外还可以判断是否反向 IsOpposite()，是否平行 IsParallel()。可参考以下代码：

//vector
AMCAX::VectorT<double, 3> v1(1.0, 2.0, 3.0);
AMCAX::VectorT<double, 3> v2(-1.0, -2.0, -3.0);
AMCAX::VectorT<double, 3> v3(2.0, 4.0, 6.0);
 
//IsOpposite
bool op1 = v1.IsOpposite(v2, 0.1);
std::cout << op1 << std::endl;
//IsParallel
bool pa1 = v1.IsParallel(v3, 0.1);
std::cout << pa1 << std::endl;
 
//direction
AMCAX::DirectionT<double, 3> d1(1.0, 2.0, 3.0);
AMCAX::DirectionT<double, 3> d2(-1.0, -2.0, -3.0);
AMCAX::DirectionT<double, 3> d3(2.0, 4.0, 6.0);
 
//IsOpposite
bool op2 = d1.IsOpposite(d2,0.1);
std::cout << op2 << std::endl;
//IsParallel
bool pa2 = d1.IsParallel(d3, 0.1);
std::cout << pa2 << std::endl;

模

Vector 可以计算其模长和对其进行归一化，与 Coord 类似。

模长

AMCAX::Vector3 vec1(0.1, 2.0, -3.3);

double length = vec1.Norm();

归一化

AMCAX::Vector3 vec1(0.1, 2.0, -3.3);
AMCAX::Vector3 vn = vec1.Normalized();
//change
vec1.Normalize();

轴

Axis3 是三维空间中的轴，等价于一个 Point3 加一个 Direction3。构建方法如下：

AMCAX::Point3 p;
AMCAX::Direction3 dir;
AMCAX::Axis3 axis(p, dir);
//Get the location and direction
AMCAX::Point3 p1 = axis.Location();
AMCAX::Direction3 dir1 = axis.Direction();

此外内核支持计算轴的角度和模长。可参考以下代码：

AMCAX::Point3 p;
AMCAX::Direction3 dir;
AMCAX::Axis3 axis(p, dir);
AMCAX::Axis3 axis2(AMCAX::Point3(1.0, 2.0, 3.0), AMCAX::Direction3(0.0, 1.0, 1.0));
double angle = axis.Angle(axis2);

标架

定义

Frame3 是三维空间中的标架，即点和 3 个互相垂直的方向。

世界坐标系{O;x,y,z}就是一个常用的标架，也是 Frame3 默认构造函数的标架：

AMCAX::Frame3 frame;
const AMCAX::Point3& p = frame.Location();
//get
const AMCAX::Direction3& x = frame.XDirection();
const AMCAX::Direction3& y = frame.YDirection();
const AMCAX::Direction3& z = frame.Direction();
 
AMCAX::Frame3 frame2(p, z, x);

注：如果输入的 z 轴与 x 轴并不垂直，算法会用 z 外积 x 得到 y，再用 y 外积 z 得到 x。

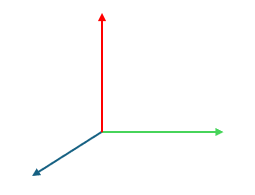
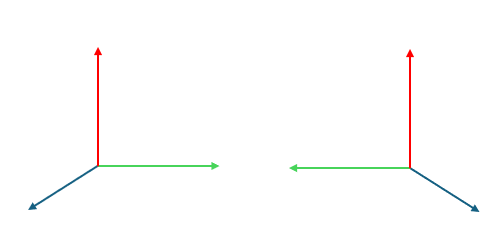
左右手系

左图为右手系，右图为左手系（图中蓝、绿、红分别表示 x、y、z 轴），常用的局部坐标系为右手系。判断左右手系的方法是将右手的手指从 x 向 y 弯曲，如果大拇指与 z 方向一致就是右手系。

我们内核获取一个标架是否为右手系的方法是：

AMCAX::Frame3 frame;

bool isRightHand = frame.IsDirect();

AMCAX::FrameT::IsDirect

constexpr bool IsDirect() const noexcept

三维标架是否为右手标架

定义 FrameT.hpp:520

局部坐标系

标架可表示一个局部坐标系。局部坐标系的优势是可以将空间曲线曲面的构建简单化。

坐标平面

XOY 平面

可以通过如下两种方式构造一个标准 XOY 平面。

//Method 1
AMCAX::Frame3 frame1 = AMCAX::CartesianCoordinateSystem::XOY();
std::cout << frame1.XDirection() << std::endl;//1 0 0
std::cout << frame1.YDirection() << std::endl;//0 1 0
std::cout << frame1.Direction() << std::endl;//0 0 1
std::cout << frame1.Location() << std::endl;//0 0 0
 
//Method 2
AMCAX::Frame3 frame2(AMCAX::Point3(0., 0., 0.), AMCAX::Direction3(0., 0., 1.), AMCAX::Direction3(1., 0., 0.));
std::cout << frame2.XDirection() << std::endl;//1 0 0
std::cout << frame2.YDirection() << std::endl;//0 1 0
std::cout << frame2.Direction() << std::endl;//0 0 1
std::cout << frame2.Location() << std::endl;//0 0 0

YOZ 平面

可以通过如下两种方式构造一个标准 YOZ 平面。

//Method 1
AMCAX::Frame3 frame4 = AMCAX::CartesianCoordinateSystem::YOZ();
std::cout << frame4.XDirection() << std::endl;//0 1 0
std::cout << frame4.YDirection() << std::endl;//0 0 1
std::cout << frame4.Direction() << std::endl;//1 0 0
std::cout << frame4.Location() << std::endl;//0 0 0
 
//Method 2
AMCAX::Frame3 frame5(AMCAX::Point3(0., 0., 0.), AMCAX::Direction3(1., 0., 0.), AMCAX::Direction3(0., 1., 0.));
std::cout << frame5.XDirection() << std::endl;//0 1 0
std::cout << frame5.YDirection() << std::endl;//0 0 1
std::cout << frame5.Direction() << std::endl;//1 0 0
std::cout << frame5.Location() << std::endl;//0 0 0

ZOX 平面

可以通过如下两种方式构造一个标准 ZOX 平面。

//Method 1
AMCAX::Frame3 frame7 = AMCAX::CartesianCoordinateSystem::ZOX();
std::cout << frame7.XDirection() << std::endl;//0 0 1
std::cout << frame7.YDirection() << std::endl;//1 0 0
std::cout << frame7.Direction() << std::endl;//0 1 0
std::cout << frame7.Location() << std::endl;//0 0 0
 
//Method 2
AMCAX::Frame3 frame8(AMCAX::Point3(0., 0., 0.), AMCAX::Direction3(0., 1., 0.), AMCAX::Direction3(0., 0., 1.));
std::cout << frame8.XDirection() << std::endl;//0 0 1
std::cout << frame8.YDirection() << std::endl;//1 0 0
std::cout << frame8.Direction() << std::endl;//0 1 0
std::cout << frame8.Location() << std::endl;//0 0 0

另外在应用中还会涉及到 Z 轴为负方向的 XOY 平面，X 轴为负方向的 YOZ 平面，Y 轴为负方向的 ZOX 平面。

Z 轴为负方向的 XOY 平面

AMCAX::Frame3 frame3_2(AMCAX::Point3(0., 0., 0.), AMCAX::Direction3(0., 0., -1.), AMCAX::Direction3(-1., 0., 0.));
std::cout << frame3_2.XDirection() << std::endl;//-1 0 0
std::cout << frame3_2.YDirection() << std::endl;//0 1 0
std::cout << frame3_2.Direction() << std::endl;//0 0 -1
std::cout << frame3_2.Location() << std::endl;//0 0 0

X 轴为负方向的 YOZ 平面

AMCAX::Frame3 frame6_2(AMCAX::Point3(0., 0., 0.), AMCAX::Direction3(-1., 0., 0.), AMCAX::Direction3(0., -1., 0.));
std::cout << frame6_2.XDirection() << std::endl;//0 -1 0
std::cout << frame6_2.YDirection() << std::endl;//0 0 1
std::cout << frame6_2.Direction() << std::endl;//-1 0 0
std::cout << frame6_2.Location() << std::endl;//0 0 0

Y 轴为负方向的 ZOX 平面

AMCAX::Frame3 frame9_2(AMCAX::Point3(0., 0., 0.), AMCAX::Direction3(0., -1., 0.), AMCAX::Direction3(0., 0., -1.));
std::cout << frame9_2.XDirection() << std::endl;//0 0 -1
std::cout << frame9_2.YDirection() << std::endl;//1 0 0
std::cout << frame9_2.Direction() << std::endl;//0 -1 0
std::cout << frame9_2.Location() << std::endl;//0 0 0

变换

大部分几何都支持变换，即平移、旋转、镜像，等比例放缩变换等。

平移变换

AMCAX::TopoShape box = AMCAX::MakeBox(AMCAX::Point3(-5.0, -5.0, 0.0), AMCAX::Point3(5.0, 5.0, 3.0));
AMCAX::Transformation3 trans;
trans.SetTranslation(AMCAX::Vector3(1.0, 0.0, 0.0));
AMCAX::TopoShape box2 = AMCAX::TransformShape(box, trans);

旋转变换

AMCAX::TopoShape box = AMCAX::MakeBox(AMCAX::Point3(-5.0, -5.0, 0.0), AMCAX::Point3(5.0, 5.0, 3.0));
AMCAX::Transformation3 trans;
trans.SetRotation(AMCAX::Axis3(), AMCAX::Constants::pi * 0.25);
AMCAX::TopoShape box3 = AMCAX::TransformShape(box, trans);

镜像变换

点镜像

AMCAX::TopoShape box = AMCAX::MakeBox(AMCAX::Point3(-5.0, -5.0, 0.0), AMCAX::Point3(5.0, 5.0, 3.0));
AMCAX::Transformation3 trans;
trans.SetMirror(AMCAX::Point3(10.,10.,10.));
AMCAX::TopoShape box4 = AMCAX::TransformShape(box, trans);

轴镜像

AMCAX::TopoShape box = AMCAX::MakeBox(AMCAX::Point3(-5.0, -5.0, 0.0), AMCAX::Point3(5.0, 5.0, 3.0));
AMCAX::Transformation3 trans;
trans.SetMirror(AMCAX::Axis3(AMCAX::Point3(10.0, 20.0, 30.0), AMCAX::Direction3(0.0, 1.0, 1.0)));
AMCAX::TopoShape box5 = AMCAX::TransformShape(box, trans);

平面镜像

AMCAX::TopoShape box = AMCAX::MakeBox(AMCAX::Point3(-5.0, -5.0, 0.0), AMCAX::Point3(5.0, 5.0, 3.0));
AMCAX::Transformation3 trans;
trans.SetMirror(AMCAX::Frame3(AMCAX::Point3(10.0, 10.0, 10.0), AMCAX::Direction3(0.0, 0.0, 1.0)));
AMCAX::TopoShape box6 = AMCAX::TransformShape(box, trans);

等比例放缩变换

AMCAX::TopoShape box = AMCAX::MakeBox(AMCAX::Point3(-5.0, -5.0, 0.0), AMCAX::Point3(5.0, 5.0, 3.0));
AMCAX::Transformation3 trans;
trans.SetScale(AMCAX::Point3(), 0.5);
AMCAX::TopoShape box7 = AMCAX::TransformShape(box, trans);

复合变换

复合变换的公式为sRx+b，其中，s为放缩因子，R为旋转矩阵，x为待变换的坐标，b为平移向量。

如构建如下变换：先绕x轴旋转pi/4，再缩放至0.2倍，最后沿x轴平移1个单位：

AMCAX::TopoShape box = AMCAX::MakeBox(AMCAX::Point3(-5.0, -5.0, 0.0), AMCAX::Point3(5.0, 5.0, 3.0));
AMCAX::Transformation3 trans;
trans.SetRotationPart(AMCAX::QuaternionT<double>(AMCAX::Coord3(1.0, 0.0, 0.0), AMCAX::Constants::pi * 0.25));
trans.SetScaleFactor(0.2);
trans.SetTranslationPart(AMCAX::Vector3(1.0, 0.0, 0.0));
AMCAX::TopoShape box8 = AMCAX::TransformShape(box, trans);

将局部坐标系的物体变为全局坐标系（或另一坐标系）的变换

构建变换使得局部坐标系f2={O=(1,0,0), OZ=(1,1,0), OX=(0,0,1)}下的物体变换为全局坐标系下的物体：

AMCAX::Frame3 f1;
AMCAX::Frame3 f2(AMCAX::Point3(1.0, 0.0, 0.0), AMCAX::Direction3(0.5, 0.5, 0.0), AMCAX::Direction3(0.0, 0.0, 1.0));
AMCAX::Transformation3 trans1;
trans1.SetTransformation(f2, f1);

将标架1平移、旋转到标架2的变换

构建变换使得全局坐标系的标架变换为另一标架f2={O=(1,0,0), OZ=(1,1,0), OX=(0,0,1)}：

AMCAX::Frame3 f1;
AMCAX::Frame3 f2(AMCAX::Point3(1.0, 0.0, 0.0), AMCAX::Direction3(0.5, 0.5, 0.0), AMCAX::Direction3(0.0, 0.0, 1.0));
AMCAX::TopoShape box11 = AMCAX::MakeBox(f1, 2.0, 2.0, 2.0);
AMCAX::Transformation3 trans2;
trans2.SetDisplacement(f1, f2);
AMCAX::TopoShape box12 = AMCAX::TransformShape(box11, trans2);

变换的乘法

trans1 * trans2。即在trans2后再用trans1进行变换。

AMCAX::TopoShape box = AMCAX::MakeBox(AMCAX::Point3(-5.0, -5.0, 0.0), AMCAX::Point3(5.0, 5.0, 3.0));
AMCAX::Transformation3 trans11;
trans11.SetScaleFactor(0.2);
AMCAX::Transformation3 trans22;
trans22.SetMirror(AMCAX::Point3(10., 10., 10.));
AMCAX::TopoShape bbox = AMCAX::TransformShape(box, trans11*trans22);