定义

参数曲线

参数曲线是通过一个参数 t 来描述的曲线，通常表示为：C(t) = (x(t),y(t),z(t))。其中：t 是参数，通常定义在某个区间 [a,b] 上。x(t)、y(t)、z(t) 是关于参数 t 的函数，分别表示曲线在三维空间中的坐标。参数曲线通过参数 t 的变化来描述曲线的形状。因为参数化方式不唯一，所以同一个曲线可以用不同的参数方程表示。
接下来我们将举一些例子。

直线： C(t) = P0 + t⋅(P1−P0) , t∈[0,1]，其中 P0 和 P1 是直线的起点和终点。
圆弧： C(t) = (rcos(t),rsin(t)) , t∈[0,2π]，其中 r 是半径。
贝塞尔曲线：

参数曲面

参数曲面是通过两个参数 u 和 v 来描述的曲面，通常表示为：S(u,v) = (x(u,v),y(u,v),z(u,v))，其中 u 和 v 是参数，通常定义在某个区域 [a,b]×[c,d] 上，x(u,v)、y(u,v)、z(u,v) 是关于参数 u 和 v 的函数，分别表示曲面在三维空间中的坐标。参数曲面通过参数 u 和 v 的变化来描述曲面的形状。因为参数化方式不唯一，所以同一个曲面可以用不同的参数方程表示。
接下来我们将举一些例子。

平面： S(u,v) = P0 + u⋅A + v⋅B, u, v∈R。其中 P0是平面上的一个点，A 和 B 是平面的两个方向向量。
球面： S(u,v) = (rsin(u)cos(v),rsin(u)sin(v),rcos(u)) ,u∈[0,π],v∈[0,2π]。其中 r 是半径。
贝塞尔曲面：

连续性

参数连续

曲线

参数连续是指曲线在连接处的参数导数连续。对于曲线来说，参数连续性涉及一阶导数、二阶导数等高阶导数。在 CAD 和几何建模中，参数连续用于确保曲线拼接的光滑性。高阶参数连续（如 C²）常用于汽车、航空航天等领域，要求曲线的曲率连续。

定义

C⁰ 连续：曲线在连接点处位置连续，但切线方向可能不连续。
C¹ 连续：曲线在连接点处位置和一阶导数（切线方向）连续。
C² 连续：曲线在连接点处位置、一阶导数和二阶导数（曲率）连续。

条件

对于两条曲线 r1(t) 和 r2(t)，在连接处 t=t0 需要满足：

C⁰ 连续：r1(t0) = r2(t0)
C¹ 连续：
C² 连续：

曲面

参数连续是指曲面在连接处的参数导数连续。对于曲面来说，参数连续性不仅涉及 u 和 v 方向的一阶导数，还涉及高阶导数。在 CAD 和几何建模中，参数连续用于确保曲面拼接的光滑性。高阶参数连续（如 C²）常用于汽车、航空航天等领域，要求曲面的曲率连续。

定义

C⁰ 连续：曲面在连接处位置连续，但法向量可能不连续。
C¹ 连续：曲面在连接处位置和一阶偏导数（切平面）连续。
C² 连续：曲面在连接处位置、一阶偏导数和二阶偏导数（曲率）连续。

条件

对于两个曲面 S1(u,v) 和 S2(u,v)，在连接处需要满足：

C⁰ 连续：
C¹ 连续：
C² 连续：

几何连续

曲线

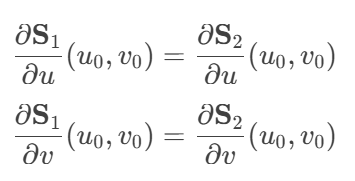
几何连续是指曲线在连接处的几何性质（如切线方向、曲率）连续，而不一定要求参数导数连续。几何连续更注重曲线的视觉效果。几何连续的条件比参数连续宽松，因此在某些情况下更容易实现。

定义

G⁰ 连续：曲线在连接点处位置连续，但切线方向可能不连续。
G¹ 连续：曲线在连接点处位置连续，且切线方向连续（切线方向相同，但大小可能不同）。
G² 连续：曲线在连接点处位置和切线方向连续，且曲率连续（曲率相同，但曲率变化率可能不同）。

条件

对于两条曲线 r1(t) 和 r2(t)，在连接处 t=t0 需要满足：

G⁰ 连续：r1(t0) = r2(t0)
G¹ 连续：T1(t0) || T2(t0)，其中 T1 和 T2 是曲线的单位切向量
G² 连续：κ1(t0) = κ2(t0)，其中 κ1 和 κ2 是曲线的曲率

在上面我们提到了曲率，参数曲线的曲率的计算公式为：

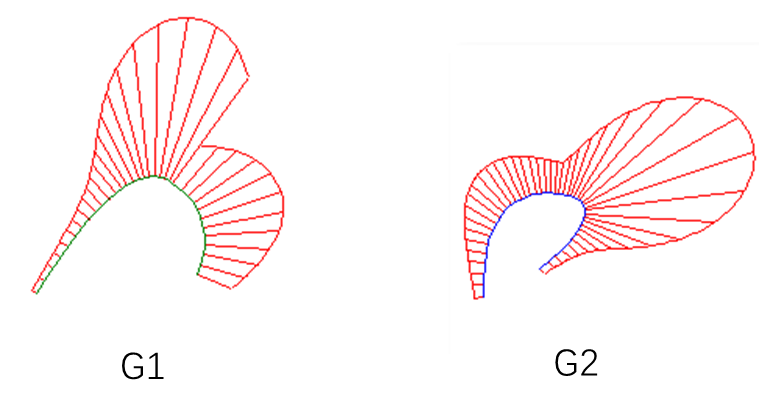
在商用软件中可以查看曲线的曲率梳，曲率连续即为 G2：

曲面

几何连续是指曲面在连接处的几何性质（如切平面、曲率）连续，而不一定要求参数导数连续。几何连续更注重曲面的视觉效果。几何连续的条件比参数连续宽松，因此在某些情况下更容易实现。

定义

G⁰ 连续：曲面在连接处位置连续，但法向量可能不连续。
G¹ 连续：曲面在连接处位置连续，且法向量连续（切平面相同，但切向量的长度可能不同）。
G² 连续：曲面在连接处位置和法向量连续，且曲率连续（所有法曲率相同，但曲率变化率可能不同）。

条件

对于两个曲面 S1(u,v) 和 S2(u,v)，在连接处需要满足：

G⁰ 连续：
G¹ 连续：

其中 n1 和 n2 是曲面的法向量。
G² 连续：

其中 κ1 和 κ2 是曲面的曲率。

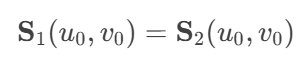
在这里补充一些内容：
1.法曲率定义
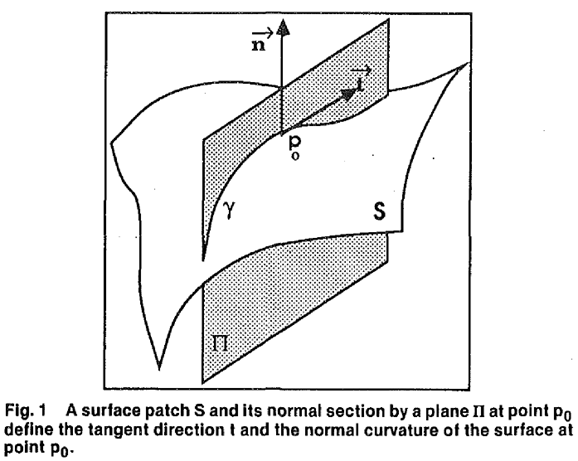
法曲率定义为曲面和某一法平面（过法向的平面）交线的曲率，如下图所示。图中曲线 γ 在 p0 点处的曲率即曲面 S 在 p0 处 t 方向的法曲率。

法曲率的定义并不易于计算。计算法曲率的简便方法为：计算方向 t 在切平面上的坐标，记为 (α,β)，即 t=αDu + βDv，则法曲率为：

其中，EFG 与曲面第一基本型中的符号含义相同；LMN 与曲面第二基本型中的符号含义相同，即：

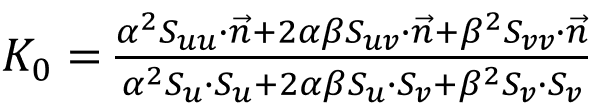
2.G2 连续即在连接曲线上任一点的所有方向法曲率都相同

但是所有方向法曲率都相同是非常强的条件，Link Curvage Theorem 证明了，只需在 1 个与 t 不共线的方向上法曲率相等，那么所有方向上的法曲率都相等。所以只考虑 t 的法向 b，只要 b 方向的法曲率是相同的，那么就 G2 连续。

3.曲面 G2 连续的表现
曲面是否 G2 连续可以通过光学效果进行近似分析。G0 的斑马线是断开的，G1 的斑马线相连但不光滑，G2 的斑马线相连且光滑。

更为实用的几何连续性表达

从上述几何连续性的定义可以推导出一些更具实用价值的结论：

1. 曲线 a 在和曲线 b 的连接点处一阶导为 d1，二阶导为 d2，若曲线 b 在连接点处一阶导为 a*d1，则 G1 连续；若曲线 b 一阶导为 a*d1 并且二阶导为 a*a*d2+b*d1，则 G2 连续，其中 a 为非负实数，b 为实数。该结论使得曲线 G2 连续可以用两个参数进行控制，并且实现方式为 C2。
2. 曲面 a 和曲面 b 在 u 边界相连且 G1 连续，曲面 a 在和曲面 b 的某一连接点处的 u 方向 1 阶导为 du，二阶导为 duu，若曲面 b 在连接点处的 u 方向一阶导为 a*du 并且二阶导为 a*a*duu + b*du，则 G2 连续，其中 a 为非负实数，b 为实数。该结论使得曲面在边界处的G2连续可以用两个参数进行控制，并且实现方式为 C2。