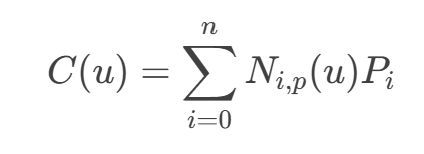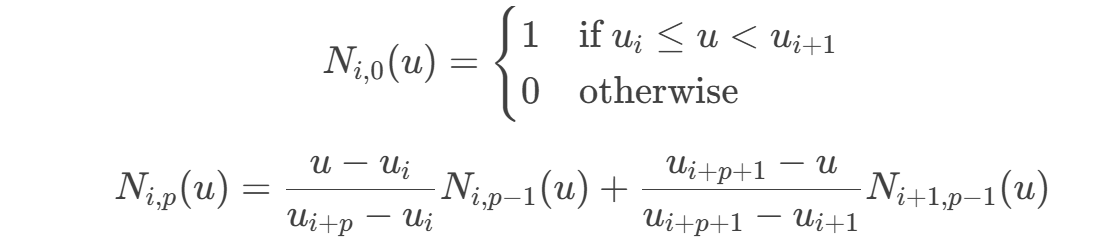B 样条的定义与构成

定义

B 样条（B-spline）是一种广泛应用于计算机图形学、几何建模和数值分析的分段多项式曲线，由控制点、节点向量和基函数构成。其数学表达式为：

其中 Pi 是控制点，用于定义曲线的形状；Ni,p(u) 是 B 样条基函数，用于将控制点加权组合成曲线；p 是 B 样条的次数；u 是参数，其取值范围由节点向量决定。

构成

B 样条的构成包括控制点、节点向量、基函数、次数、权重。

控制点

控制点是 B 样条曲线的几何定义点，决定了曲线的形状和走向。

节点向量

节点向量是一个非递减的实数序列 U={u0,u1,…,um}，用于定义参数空间的分段区间，节点向量可以是均匀的（节点间隔相等）或非均匀的（节点间隔可以不相等）。在这里会涉及到节点重数，节点重数是节点向量中某个节点值的重复次数。例如，节点向量 {0,0,0,1,2,2,3} 中：节点 0 的重数为 3，节点 1 的重数为 1，节点 2 的重数为 2，节点 3 的重数为 1。

基函数

B 样条基函数 Ni,p(u) 通过递归公式计算：

基函数决定了控制点对曲线形状的贡献。

次数

次数 p 是 B 样条的多项式次数。次数越高，曲线的光滑性越好。

权重

标准 B 样条是没有权重的，所有控制点的权重默认为 1。而有理 B 样条（NURBS）引入了权重，使得曲线可以表示更复杂的几何形状（如圆锥曲线），权重可以调整控制点对曲线形状的影响。

B 样条的分类

B 样条（B-spline）可以根据不同的特性进行分类，常见的分类包括均匀 B 样条、非均匀 B 样条、周期 B 样条、非周期 B 样条和有理 B 样条（NURBS）。以下是它们的详细介绍：

均匀 B 样条

均匀 B 样条的节点向量沿参数轴是均匀等距分布的，即 ui+1-ui=常数（>0）。例如节点向量：{0,1,2,3,4,5,6}，节点之间的间隔为 1。

非均匀 B 样条

非均匀 B 样条的节点向量是非均匀分布的，即节点之间的间隔可以不相等。节点向量的形式可以是任意的非递减序列，例如 {0,0.5,1.2,2.0,3.5}。

周期 B 样条

周期 B 样条的节点向量是周期性的，即曲线在参数域的两端是连续的，通常用于表示闭合曲线。需要注意的是：周期 B 样条曲线的节点向量首尾的重数相等，且控制点数目 = 节点重数之和 - 最后一个节点的重数。对于周期 B 样条，不需要满足 m= n + p + 1。

std::vector< AMCAX::Point3 > pts2;
pts2.push_back(AMCAX::Point3(0., 0., 0.));
pts2.push_back(AMCAX::Point3(1., 1., 0.));
pts2.push_back(AMCAX::Point3(2., 2., 2.));
pts2.push_back(AMCAX::Point3(3., -5., 0.));
pts2.push_back(AMCAX::Point3(0., 0., 0.));
 
const std::vector< double > knots2 = { 0.,0.5, 1.,1.5, 2.0, 2.5};
const std::vector< int > multiplicities2 = { 1, 1, 1, 1, 1, 1};
 
int degree2 = 4;
std::shared_ptr< AMCAX::Geom3BSplineCurve> bspline2 = std::make_shared< AMCAX::Geom3BSplineCurve>(pts2, knots2, multiplicities2, degree2, true);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge(bspline2), "bspline2.brep");

在上面这个例子中，节点向量首尾的重数都为 1，控制点数目 = 节点重数之和 - 最后一个节点的重数，即均为 5。

非周期 B 样条

非周期 B 样条的节点向量是非周期性的，曲线在参数域的两端通常与控制点的首尾点重合，通常用于表示开放曲线。

std::vector< AMCAX::Point3 > pts1;
pts1.push_back(AMCAX::Point3(0.,0.,0.));
pts1.push_back(AMCAX::Point3(1.,1.,0.));
pts1.push_back(AMCAX::Point3(2.,2.,2.));
pts1.push_back(AMCAX::Point3(3.,-5.,0.));
const std::vector< double > knots1 = { 1.,2. };
const std::vector< int > multiplicities1 = { 4,4 };
int degree = 3;
std::shared_ptr< AMCAX::Geom3BSplineCurve> bspline1 = std::make_shared< AMCAX::Geom3BSplineCurve>(pts1, knots1, multiplicities1, degree, false);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge(bspline1), "bspline1.brep");

在上面这个例子中，控制点数目为 4，曲线次数为 3，节点重数之和为 8，节点向量的总和满足 m=n+p+1。

有理 B 样条（NURBS）

有理 B 样条是 B 样条的推广，支持更复杂的几何形状。NURBS 在 B 样条的基础上引入了权重（正数），使得曲线可以表示圆锥曲线（如圆、椭圆、抛物线等），而权重可以调整曲线的形状，使其更灵活。

std::vector<AMCAX::Point3> pts3 = {
AMCAX::Point3(0., 0., 0.),
AMCAX::Point3(1., 1., 0.),
AMCAX::Point3(2., 2., 2.),
AMCAX::Point3(3., -5., 0.)
};
 
std::vector<double> knots3 = {1., 2., 3., 4.};
std::vector<int> mults3 = { 2, 2, 2, 2};
std::vector<double> weights3 = { 1., 2., 1., 1.};
 
std::shared_ptr<AMCAX::Geom3BSplineCurve> bspline3 = std::make_shared<AMCAX::Geom3BSplineCurve>(pts3, weights3, knots3, mults3, 3, false, true);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge(bspline3), "bspline3.brep");
std::cout << bspline3->IsRational() << std::endl;//1

对于一个有理 B 样条而言，权重需要大于 0 且不相同，如果所有权重相等，则有理 B 样条将会退化为非有理 B 样条。

如何构建一个合法的 B 样条

要想构建一个合法的 B 样条需要满足以下条件：

1.控制点

至少需要 p+1 个控制点。例如，对于 3 次 B 样条，控制点的数量至少为 4。

2.节点向量

节点向量的总和必须满足 m=n+p+1，其中 n 为控制点的数目，p 为曲线次数。（非周期情况下）
节点向量必须是非递减的。

3.节点重数

对于非周期 B 样条，节点向量首尾的重数相等，且去掉最后一个节点的重数之和等于控制点数量。
节点重数的数组大小与节点向量的数组大小相等。

B 样条的重要性质

端点处的切向与控制点间的关系

对于非周期 B 样条，曲线在端点处的切向与控制点的方向一致。而对于周期 B 样条，曲线在端点处的切向通常不直接与控制点相关，因为曲线是闭合的。接下来将举一个非周期 B 样条的例子：

std::vector< AMCAX::Point3 > pts1;
pts1.push_back(AMCAX::Point3(0.,0.,0.));
pts1.push_back(AMCAX::Point3(1.,1.,0.));
pts1.push_back(AMCAX::Point3(2.,2.,2.));
pts1.push_back(AMCAX::Point3(3.,-5.,0.));
const std::vector< double > knots1 = { 1.,2. };
const std::vector< int > multiplicities1 = { 4,4 };
int degree = 3;
std::shared_ptr< AMCAX::Geom3BSplineCurve> bspline1 = std::make_shared< AMCAX::Geom3BSplineCurve>(pts1, knots1, multiplicities1, degree, false);
AMCAX::OCCTIO::OCCTTool::Write(AMCAX::MakeEdge(bspline1), "bspline1.brep");
 
double fp = bspline1->FirstParameter();
AMCAX::Point3 fpoint;
AMCAX::Vector3 fv;
bspline1->D1(fp, fpoint,fv);
std::cout << "First parameter: " << fp << std::endl;
std::cout << "Start point: " << fpoint << std::endl;
std::cout << "Start tangent: " << fv << std::endl;
 
AMCAX::Vector3 direction(
    pts1[1].X() - pts1[0].X(),
    pts1[1].Y() - pts1[0].Y(),
    pts1[1].Z() - pts1[0].Z()
);
std::cout << direction << std::endl;
 
if (fv.Normalized().IsEqual(direction.Normalized(), AMCAX::Precision::Confusion(), AMCAX::Precision::Angular()))
{
    std::cout << "The start tangent is consistent with the control point direction" << std::endl;
}
else {
    std::cout << "The start tangent is not consistent with the control point direction" << std::endl;
}

节点处的重数对连续性的影响

节点重数对曲线的连续性有着直接影响。节点重数越大，曲线在该点处的连续性越低。如果某个节点的节点重数为 1，那么曲线在该节点处是 Cp−1连续的；如果节点重数为 k，那么曲线在该节点处是 Cp−k 连续的；如果节点重数等于 p+1，那么曲线在该节点处不连续。
以 3 次 B 样条为例（p=3）：

节点重数为 1：曲线在该节点处是 C2 连续的。
节点重数为 2：曲线在该节点处是 C1 连续的。
节点重数为 3：曲线在该节点处是 C0 连续的。
节点重数为 4：曲线在该节点处不连续。

仿射不变性

B 样条具有仿射不变性，即对控制点进行仿射变换（如平移、旋转、缩放）后，曲线的形状会相应变换，但曲线的参数化形式不变，只是曲线的几何形状发生了相应的变换。这意味着无论如何对控制点应用仿射变换，B 样条曲线的形状和相对结构都会始终保持不变。