概述

本教程提供了 AMCAX 几何约束求解器的基本用法。

所需知识

开发人员需要具备一些基础知识，包括现代 C++ 编程语言、3D 几何建模概念。具体来说，AMCAX 几何约束求解器是使用 C++ 17 标准设计的，且使用 STL 容器和算法作为基本数据结构。

3D几何约束求解示例

结果预览

本示例使用两个立方体来展现 AMCAX 3D几何约束求解器的求解功能。结果如下图所示:

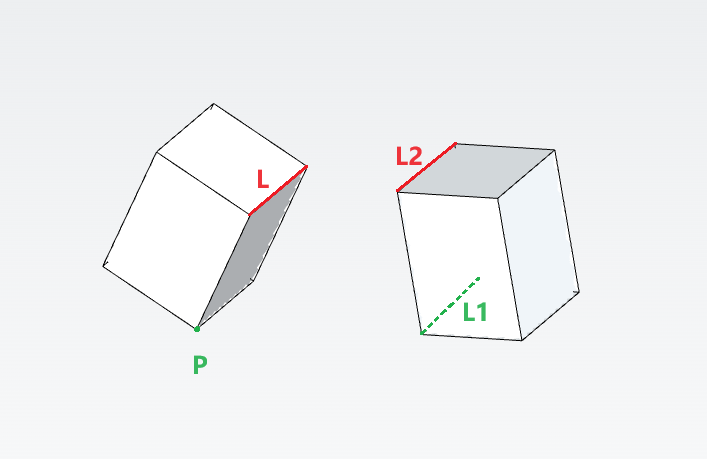
受约束的立方体

两个立方体之间存在两处约束关系:

顶点P与边L1距离为2；
边L与边L2距离为1.5。

我们将介绍如何构造几何体之间的约束关系并获取求解结果。

构造几何约束

创建刚体

第一步是创建分别代表两个立方体的刚体。

auto gcsSystem = std::make_shared<AMCAX::GCS::GCSWSystem>();
auto rigidBody1 = gcsSystem->CreateRigidBody(1);
auto rigidBody2 = gcsSystem->CreateRigidBody(2);

创建几何实体

接下来创建与几何约束相关的几何实体。

auto createPoint = [](double x, double y, double z)->AMCAX::GCS::Point3d {
    AMCAX::GCS::Point3d point;
    point.x = x;
    point.y = y;
    point.z = z;
    return point;
    };
auto createVector = [](double x, double y, double z)->AMCAX::GCS::Vector3d {
    AMCAX::GCS::Vector3d vector;
    vector.x = x;
    vector.y = y;
    vector.z = z;
    return vector;
    };
auto createLine = [](const AMCAX::GCS::Point3d& origin, const AMCAX::GCS::Vector3d& direction)->AMCAX::GCS::Line3d {
    AMCAX::GCS::Line3d line;
    line.origin = origin;
    line.direction = direction;
    return line;
    };

首先创建代表P以及L1的点与线。

auto pointCube1 = createPoint(1.2470916419629932, 0.23514982144115493, -5.820766091346741e-11);
 
auto line1Cube2 = createLine(createPoint(2.5834565193285233, 0.3538446011985319, -5.8207660913467394e-11), createVector(0.0, -1.0, 0.0));

接着创建代表L以及L2的两条线。

auto lineCube1 = createLine(createPoint(1.2470916419629932, 0.6242608214411551, 0.9999999999417923), createVector(0.0, 1.0, 0.0));

auto line2Cube2 = createLine(createPoint(2.5834565193285233, 0.3538446011985319, 0.9999999999417923), createVector(0.0, -1.0, 0.0));

创建约束关系

现在可以创建几何实体间的约束关系。

首先创建P与L1之间的距离约束，将存在约束关系的几何实体与所在刚体作为参数传入GCSSystem。

AMCAX::GCS::GCSWConHandle conHandle1;

gcsSystem->Create3dDistPtLn(conHandle1, rigidBody1, rigidBody2, pointCube1, line1Cube2, 2);

AMCAX::GCS::GCSWConHandle

GCSConHandle 的包装器

定义 AMCAXGCS.h:268

通过同样的方式创建L与L2之间的距离约束。

AMCAX::GCS::GCSWConHandle conHandle2;

gcsSystem->Create3dDistLnLn(conHandle2, rigidBody1, rigidBody2, lineCube1, line2Cube2, 1.5, AMCAX::GCS::kParallel);

求解约束关系

执行求解

完成构造约束关系后，我们可以求解刚体变换以满足上述约束。

AMCAX::GCS::Status solveStatus = gcsSystem->Solve();

获取结果

如果求解器返回结果表示求解成功，以下是获取满足约束关系的几何实体示例。

// update point on cube1
pointCube1 = gcsSystem->UpdatePoint3dPosition(rigidBody1, pointCube1);
// update line on cube1
lineCube1 = gcsSystem->UpdateLine3dPosition(rigidBody1, lineCube1);
// update the first line on cube2
line1Cube2 = gcsSystem->UpdateLine3dPosition(rigidBody2, line1Cube2);
// update the second line on cube2
line2Cube2 = gcsSystem->UpdateLine3dPosition(rigidBody2, line2Cube2);

示例代码

下面列出了此示例的完整代码：

#include <AMCAXGCS.h>
 
void RunDemo() {
    auto gcsSystem = std::make_shared<AMCAX::GCS::GCSWSystem>();
    // create rigid body for cube 1
    auto rigidBody1 = gcsSystem->CreateRigidBody(1);
    // create rigid body for cube 2
    auto rigidBody2 = gcsSystem->CreateRigidBody(2);
 
    auto createPoint = [](double x, double y, double z)->AMCAX::GCS::Point3d {
        AMCAX::GCS::Point3d point;
        point.x = x;
        point.y = y;
        point.z = z;
        return point;
        };
    auto createVector = [](double x, double y, double z)->AMCAX::GCS::Vector3d {
        AMCAX::GCS::Vector3d vector;
        vector.x = x;
        vector.y = y;
        vector.z = z;
        return vector;
        };
    auto createLine = [](const AMCAX::GCS::Point3d& origin, const AMCAX::GCS::Vector3d& direction)->AMCAX::GCS::Line3d {
        AMCAX::GCS::Line3d line;
        line.origin = origin;
        line.direction = direction;
        return line;
        };
    
    // create point on cube 1
    auto pointCube1 = createPoint(1.2470916419629932, 0.23514982144115493, -5.820766091346741e-11);
    // create first line on cube 2
    auto line1Cube2 = createLine(createPoint(2.5834565193285233, 0.3538446011985319, -5.8207660913467394e-11), createVector(0.0, -1.0, 0.0));
    
    // create line on cube 1
    auto lineCube1 = createLine(createPoint(1.2470916419629932, 0.6242608214411551, 0.9999999999417923), createVector(0.0, 1.0, 0.0));
    // create second line on cube 2
    auto line2Cube2 = createLine(createPoint(2.5834565193285233, 0.3538446011985319, 0.9999999999417923), createVector(0.0, -1.0, 0.0));
    
    // create distance constraint between point and line
    AMCAX::GCS::GCSWConHandle conHandle1;
    gcsSystem->Create3dDistPtLn(conHandle1, rigidBody1, rigidBody2, pointCube1, line1Cube2, 2);
    // create distance constraint between two lines
    AMCAX::GCS::GCSWConHandle conHandle2;
    gcsSystem->Create3dDistLnLn(conHandle2, rigidBody1, rigidBody2, lineCube1, line2Cube2, 1.5, AMCAX::GCS::kParallel);
    
    // solve the constraint problem
    AMCAX::GCS::Status solveStatus = gcsSystem->Solve();
    if (AMCAX::GCS::Status::kSolved == solveStatus) {
        // update point on cube1
        pointCube1 = gcsSystem->UpdatePoint3dPosition(rigidBody1, pointCube1);
        // update line on cube1
        lineCube1 = gcsSystem->UpdateLine3dPosition(rigidBody1, lineCube1);
        // update the first line on cube2
        line1Cube2 = gcsSystem->UpdateLine3dPosition(rigidBody2, line1Cube2);
        // update the second line on cube2
        line2Cube2 = gcsSystem->UpdateLine3dPosition(rigidBody2, line2Cube2);
    }
}

2D几何约束求解示例

本示例使用线段与圆展现 AMCAX 2D几何约束求解器的求解功能。

构造几何约束

创建几何实体

首先创建与几何约束相关的几何实体。

线段由两个端点表示，所以先创建两个端点，再由两个端点创建线段。

AMCAX::GCS::GCSWSystem gcsSystem;
AMCAX::GCS::GCSWVarGeomHandle handlePoint0;
AMCAX::GCS::GCSWVarGeomHandle handlePoint1;
gcsSystem.Create2dPoint(handlePoint0, { -63.296707, -22.307692 });
gcsSystem.Create2dPoint(handlePoint1, { -23.956042, 37.472527 });
AMCAX::GCS::GCSWVarGeomHandle handleLine;
gcsSystem.Create2dLine(handleLine, handlePoint0, handlePoint1);

圆由圆心以及半径表示，所以先创建圆心，再由圆心与半径创建圆。

AMCAX::GCS::GCSWVarGeomHandle handleCenter;
gcsSystem.Create2dPoint(handleCenter, { 23.516476, -22.087912 });
AMCAX::GCS::GCSWVarGeomHandle handleCircle;
gcsSystem.Create2dCircle(handleCircle, handleCenter, 39.189965);

创建约束关系

现在可以创建线段与圆之间的相切约束。最后一个参数0表示线段与圆周之间距离为0。

AMCAX::GCS::GCSWConHandle conHandle;

gcsSystem.Create2dTanLnCir(conHandle, handleLine, handleCircle, 0);

AMCAX::GCS::GCSWSystem::Create2dTanLnCir

Status Create2dTanLnCir(GCSWConHandle &h, GCSWVarGeomHandle &ln, GCSWVarGeomHandle &cir, double d)

二维中，创建线和圆相切约束

求解约束关系

执行求解

完成构造约束关系后，我们可以求解几何实体的位置以满足上述约束。

AMCAX::GCS::Status solveStatus = gcsSystem.Solve();

AMCAX::GCS::GCSWSystem::Solve

Status Solve()

常规求解。求解约束系统

获取结果

如果求解器返回结果表示求解成功，以下是获取满足约束关系的几何实体示例。

AMCAX::GCS::Line2d line = gcsSystem.GetLine2d(handleLine);

AMCAX::GCS::Circle2d circle = gcsSystem.GetCircle2d(handleCircle);

AMCAX::GCS::GCSWSystem::GetCircle2d

Circle2d GetCircle2d(const GCSWVarGeomHandle &h) const

获取圆

AMCAX::GCS::GCSWSystem::GetLine2d

Line2d GetLine2d(const GCSWVarGeomHandle &h) const

获取线段

AMCAX::GCS::Circle2d

二维圆

定义 AMCAXGCS.h:126

AMCAX::GCS::Line2d

二维线段

定义 AMCAXGCS.h:118

示例代码

下面列出了此示例的完整代码：

#include <AMCAXGCS.h>
 
void Run2DDemo() {
    AMCAX::GCS::GCSWSystem gcsSystem;
    AMCAX::GCS::GCSWVarGeomHandle handlePoint0;
    AMCAX::GCS::GCSWVarGeomHandle handlePoint1;
    gcsSystem.Create2dPoint(handlePoint0, { -63.296707, -22.307692 });
    gcsSystem.Create2dPoint(handlePoint1, { -23.956042, 37.472527 });
    AMCAX::GCS::GCSWVarGeomHandle handleLine;
    gcsSystem.Create2dLine(handleLine, handlePoint0, handlePoint1);
    AMCAX::GCS::GCSWVarGeomHandle handleCenter;
    gcsSystem.Create2dPoint(handleCenter, { 23.516476, -22.087912 });
    AMCAX::GCS::GCSWVarGeomHandle handleCircle;
    gcsSystem.Create2dCircle(handleCircle, handleCenter, 39.189965);
    AMCAX::GCS::GCSWConHandle conHandle;
    gcsSystem.Create2dTanLnCir(conHandle, handleLine, handleCircle, 0);
    AMCAX::GCS::Status solveStatus = gcsSystem.Solve();
    if (AMCAX::GCS::Status::kSolved == solveStatus) {
        AMCAX::GCS::Line2d line = gcsSystem.GetLine2d(handleLine);
        AMCAX::GCS::Circle2d circle = gcsSystem.GetCircle2d(handleCircle);
    }
}