Parametric Curves and Parametric Surfaces

Definition

Parametric Curves

A parametric curve is described by a parameter t, typically represented as:C(t) = (x(t),y(t),z(t)).Here:t is the parameter, usually defined over an interval [a,b] 上。x(t)、y(t)、z(t) are functions of the parameter t, representing the coordinates of the curve in three-dimensional space.The shape of the curve is described by the variation of the parameter t. Since the parameterization is not unique, the same curve can be represented by different parametric equations.
Below are some examples:

• Line: C(t) = P0 + t⋅(P1−P0) , t∈[0,1]，where P0 and P1 are the start and end points of the line.
• Circular Arc: C(t) = (rcos(t),rsin(t)) , t∈[0,2π]，where r is the radius.
• Bézier Curve:
  

Parametric Surfaces

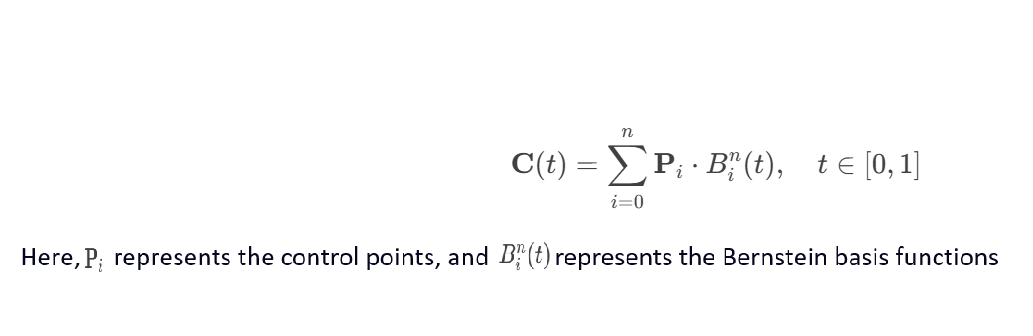
A parametric surface is described by two parameters u and v, typically represented as：S(u,v) = (x(u,v),y(u,v),z(u,v))，here u and v are parameters, usually defined over a domain [a,b]×[c,d]，x(u,v)、y(u,v)、z(u,v) are functions of the parameters u and v, representing the coordinates of the surface in three-dimensional space.The shape of the surface is described by the variation of the parameters u and v. Since the parameterization is not unique, the same surface can be represented by different parametric equations.
Below are some examples:

• Plane: S(u,v) = P0 ​+ u⋅A + v⋅B, u, v∈R ,where P0is a point on the plane, and A and B are the direction vectors of the plane.
• Sphere: S(u,v) = (rsin(u)cos(v),rsin(u)sin(v),rcos(u)) ,u∈[0,π],v∈[0,2π],where r is the radius.
• Bézier Surface:
  

Continuity

Parametric Continuity

Curves

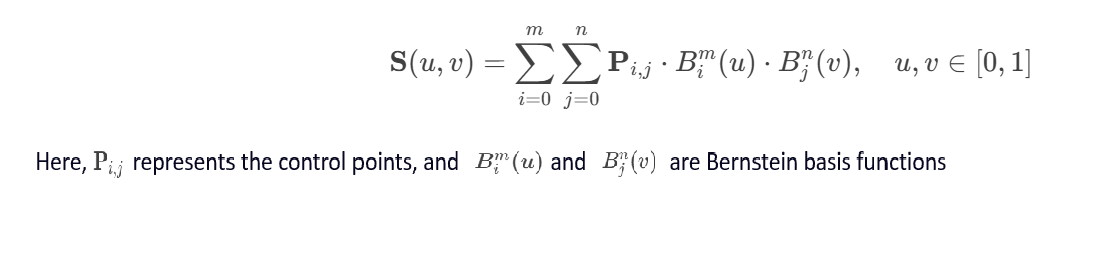
Parametric continuity refers to the continuity of the parametric derivatives at the junction of curves. For curves, parametric continuity involves first-order, second-order, and higher-order derivatives. In CAD and geometric modeling, parametric continuity ensures smooth connections between curves. Higher-order parametric continuity (e.g., C2) is often used in fields like automotive and aerospace, where curvature continuity is required.

Definition

• C⁰ Continuity: The curves are positionally continuous at the junction, but the tangent directions may not be continuous.
• C¹ Continuity: The curves are positionally and tangentially continuous at the junction (first-order derivatives are continuous).
• C² Continuity: The curves are positionally, tangentially, and curvature continuous at the junction (second-order derivatives are continuous).

Conditions

For two curves r1(t) and r2(t)，at the junction t=t0 ：

• C⁰ Continuity: r1(t0) = r2(t0)
• C¹ Continuity:
  
• C² Continuity:
  

Surfaces

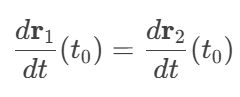
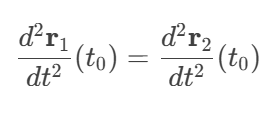
Parametric continuity refers to the continuity of the parametric derivatives at the junction of surfaces. For surfaces, parametric continuity involves first-order and higher-order partial derivatives in both u and v directions. In CAD and geometric modeling, parametric continuity ensures smooth connections between surfaces. Higher-order parametric continuity (e.g., C2) is often used in fields like automotive and aerospace, where curvature continuity is required.

Definition

• C⁰ Continuity: The surfaces are positionally continuous at the junction, but the normal vectors may not be continuous.
• C¹ Continuity: The surfaces are positionally and tangentially continuous at the junction (first-order partial derivatives are continuous).
• C² Continuity: The surfaces are positionally, tangentially, and curvature continuous at the junction (second-order partial derivatives are continuous).

Conditions

For two surfaces S1(u,v) and S2(u,v)，at the junction:

• C⁰ Continuity:
  
• C¹ Continuity:
  
• C² Continuity:
  

Geometric Continuity

Curves

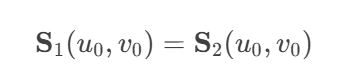
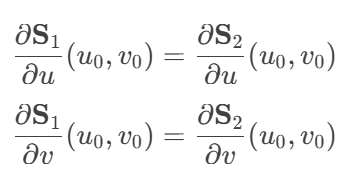
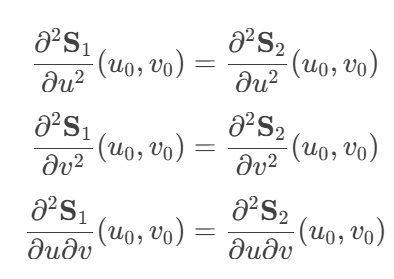
Geometric continuity refers to the continuity of geometric properties (e.g., tangent direction, curvature) at the junction of curves, without necessarily requiring parametric derivative continuity. Geometric continuity focuses more on the visual smoothness of the curves. The conditions for geometric continuity are less strict than parametric continuity, making it easier to achieve in some cases.

Definition

• G⁰ Continuity: The curves are positionally continuous at the junction, but the tangent directions may not be continuous.
• G¹ Continuity: The curves are positionally continuous at the junction, and the tangent directions are continuous (the directions are the same, but the magnitudes may differ).
• G² Continuity: The curves are positionally and tangentially continuous at the junction, and the curvature is continuous (the curvature values are the same, but the curvature rates may differ).

Conditions

For two curves r1(t) and r2(t)， at the junction t=t0:

• G⁰ Continuity: r1(t0) = r2(t0)
• G¹ Continuity: T1(t0) || T2(t0),where T1 and T2 are the unit tangent vectors of the curves.
• G² Continuity: κ1(t0) = κ2(t0),where κ1 and κ2 are the curvatures of the curves.

The curvature of a parametric curve is calculated as:

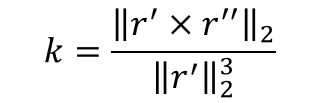
In commercial software, the curvature comb of a curve can be visualized. Curvature continuity corresponds to G2：

Surfaces

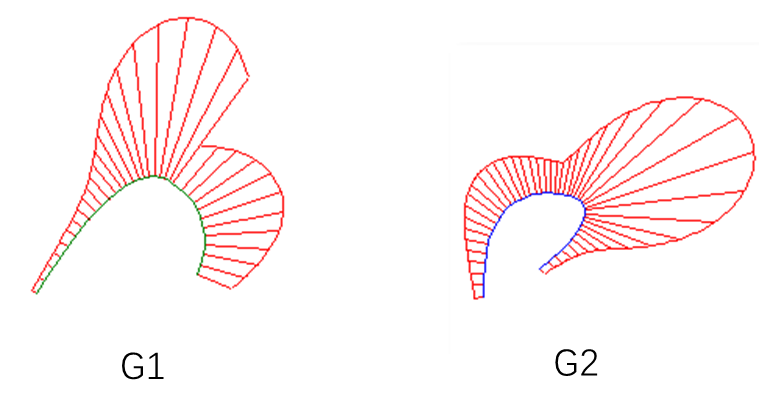
Geometric continuity refers to the continuity of geometric properties (e.g., tangent plane, curvature) at the junction of surfaces, without necessarily requiring parametric derivative continuity. Geometric continuity focuses more on the visual smoothness of the surfaces. The conditions for geometric continuity are less strict than parametric continuity, making it easier to achieve in some cases.

Definition

• G⁰ Continuity: The surfaces are positionally continuous at the junction, but the normal vectors may not be continuous.
• G¹ Continuity: The surfaces are positionally continuous at the junction, and the normal vectors are continuous (the tangent planes are the same, but the tangent vector magnitudes may differ).
• G² Continuity: The surfaces are positionally and normally continuous at the junction, and the curvature is continuous (all normal curvatures are the same, but the curvature rates may differ).

Conditions

For two surfaces S1(u,v) and S2(u,v)，at the junction:

• G⁰ Continuity:
  
• G¹ Continuity:
  
  where n1 and n2 are the normal vectors of the surfaces.
• G² Continuity:
  
  where κ1 and κ2 are the curvatures of the surfaces.

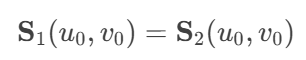
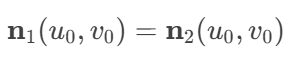
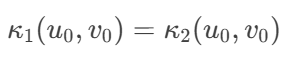
Additional Notes:
1.Normal Curvature Definition
The normal curvature is defined as the curvature of the intersection curve between the surface and a normal plane (a plane containing the normal vector). The curvature of the curve γ at point p0 is the normal curvature of the surface S at p0 in the direction t.

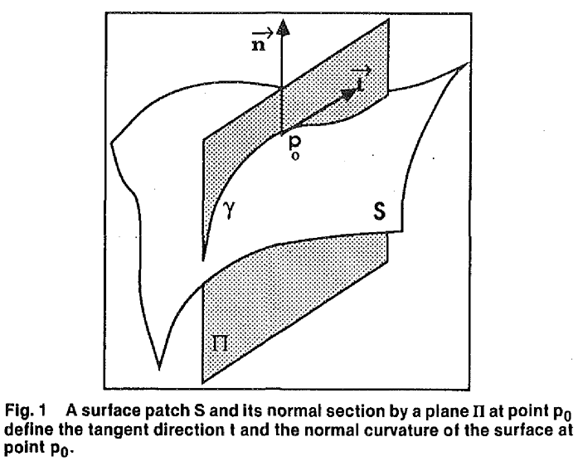
The definition of normal curvature is not easy to calculate. A convenient method to compute the normal curvature is to calculate the coordinates of direction t in the tangent plane, denoted as (α, β), where t = αDu + βDv. The normal curvature is then given by:

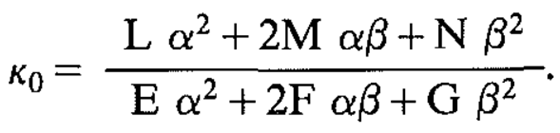
Here, EFG has the same symbolic meaning as in the first fundamental form of the surface, and LMN has the same symbolic meaning as in the second fundamental form of the surface, i.e.:

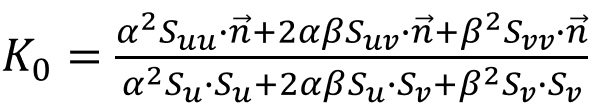
2.G2 Continuity means that the normal curvature in all directions at any point on the connecting curve is the same.

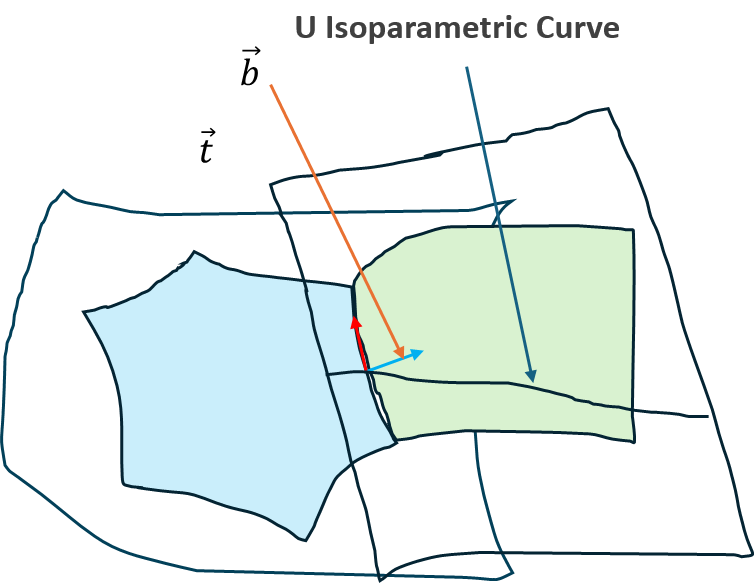
However, requiring the normal curvature in all directions to be the same is a very strong condition. The Link Curvature Theorem proves that if the normal curvature is equal in one direction that is not collinear with t, then the normal curvature in all directions will be equal. Therefore, by considering only the normal vector b of t, if the normal curvature in the b direction is the same, then the curve is G2 continuous.

3.Manifestation of Surface G2 Continuity
Whether a surface is G2 continuous can be approximated by optical effects. The zebra stripes for G0 continuity are broken, for G1 continuity, the stripes are connected but not smooth, and for G2 continuity, the stripes are connected and smooth.

More Practical Expressions of Geometric Continuity

From the definitions of geometric continuity, some more practical conclusions can be derived:

• 1. For curve a and curve b at their connection point, if the first derivative at the connection point is d1 and the second derivative is d2, then if the first derivative of curve b at the connection point is a * d1, it is G1 continuous. If the first derivative of curve b is a * d1 and the second derivative is a * a * d2 + b * d1, then it is G2 continuous, where a is a non-negative real number and b is a real number. This conclusion shows that the G2 continuity of a curve can be controlled by two parameters, and the implementation is C2.
  
• 2. If surface a and surface b are connected at the u boundary and are G1 continuous, and at a connection point on surface a, the first derivative in the u direction is du and the second derivative is duu, and the first derivative of surface b at the connection point in the u direction is a * du, and the second derivative is a * a * duu + b * du, then it is G2 continuous, where a is a non-negative real number and b is a real number. This conclusion shows that the G2 continuity at the boundary of a surface can be controlled by two parameters, and the implementation is C2.