
|
AMCAX Kernel 1.0.0.0
|

|
AMCAX Kernel 1.0.0.0
|
Using the default constructor will result in the origin of coordinates. You need to input floating-point numbers when constructing. Also, all geometries only support input of floating-point numbers, which will not be specifically mentioned in the future.
You can use the following two methods to get the value of a particular dimension of the coordinate.
You can modify the value of a particular dimension of the coordinate using the following two methods.
Support addition, subtraction, scalar multiplication, dot product, cross product, and also support == and !=.
== and != can be used to compare coordinates and their respective dimensions.
The kernel support calculating the norm (magnitude) of the coordinate and normalizing the coordinate.
There are two ways to normalize a coordinate: one does not change the coordinate itself and creates a new coordinate, while the other directly modifies the coordinate.
The kernel support outputting coordinates using << and inputting with >>.
Using the default constructor will result in the origin. It can either be directly created or constructed based on Coord3/Coord2.
You can use the following two methods to get the value of a particular dimension of the point.
You can modify the value of a particular dimension of the point using the following two methods.
The kernel does not support arithmetic operations (addition, subtraction, multiplication, division) on points. In fact, most geometries do not support arithmetic operations, except for Coord. This will not be explained further. However, if you need to perform arithmetic on points, you can first obtain the point's Coord, then perform operations on the Coord:
Most geometries support transformations such as translation, rotation, mirror, and scale, which will not be explained further.
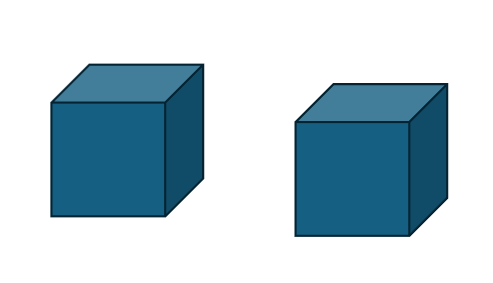
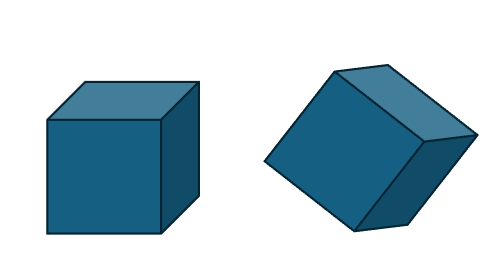
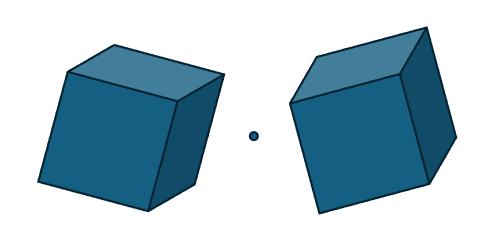
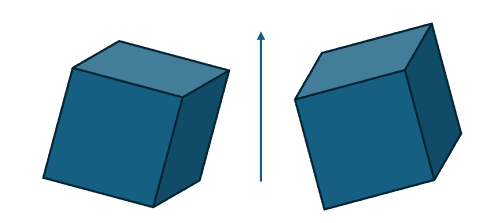
The formula for composite transformation is sRx+bsRx+b, where ss is the scaling factor, RR is the rotation matrix, xx is the coordinate to be transformed, and bb is the translation vector.
For example, constructing the following transformation: first rotate around the x-axis by π/4π/4, then scale by a factor of 0.2, and finally translate 1 unit along the x-axis:
Construct a transformation so that the object in the local coordinate system f2={O=(1,0,0), OZ=(1,1,0), OX=(0,0,1)}is transformed to the global coordinate system:
Construct a transformation to change the global coordinate frame to another frame f2={O=(1,0,0), OZ=(1,1,0), OX=(0,0,1)}:
trans1 * trans2。which applies trans2 first, then trans1:
Vector3 refers to a mathematical vector with both direction and length, while Direction3 has only direction, with a magnitude of 1.0.
The access and modification methods for vectors and directions are similar to the Coord class, except that directions are automatically normalized.
To get a particular dimension's value of a vector or direction:
To modify a particular dimension's value of a vector or direction:
Vectors can be added, subtracted, and scaled by a number. Directions do not support addition and subtraction. Both vectors and directions support dot and cross products, similar to the Coord class.
The kernel supports computing angles. The Angle() method calculates the angle between vectors, with a range of [0.0, pi]. The AngleWithRef() method computes the angle with a reference direction in 2D, with a range of [-pi, pi]. The sign of the angle depends on whether the coordinate system is right-handed or left-handed.
Note: In 2D, only Angle() should be used to calculate rotation.
Additionally, the methods IsOpposite() and IsParallel() can be used to check if vectors or directions are opposite or parallel:
Vector can compute their magnitude and be normalized, similar to the Coord class.
Axis3 is an axis in 3D space, equivalent to a Point3 plus a Direction3. Construction is as follows:
The kernel also supports computing the angle and magnitude of axis:
Frame3 is a frame in 3D space, consisting of a point and three mutually perpendicular directions.
The world coordinate system {O; x, y, z} is a commonly used frame, and the default constructor of Frame3 creates this frame:
Note: If the input z-axis is not perpendicular to the x-axis, the algorithm will compute the y-axis as the cross product of z and x, and compute x as the cross product of y and z.
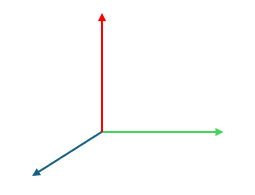
The left image shows a right-handed system, and the right image shows a left-handed system (with blue, green, and red representing the x, y, and z axes respectively). The most common local coordinate system is the right-handed system. To determine if a frame is right-handed, curl the fingers of the right hand from x to y, and if the thumb points in the z direction, it is a right-handed system.
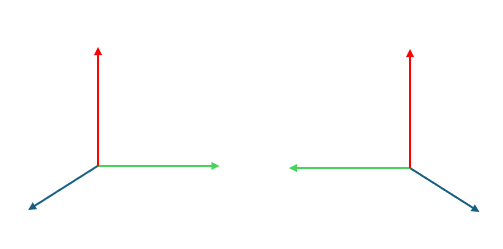
The way we kernel to get whether a standard frame is right-handed or not is:
A frame can represent a local coordinate system, which simplifies the construction of spatial curves and surfaces.
There are three main transformations: transforming from a local coordinate system to the global coordinate system, transforming from one local coordinate system to another, and constructing affine transformations to translate, rotate, or mirror one frame to another. Refer to the transformation section above for more details.
AMCAX::Geom3Curve::FirstParameter is used to obtain the starting parameter of the curve, and AMCAX::Geom3Curve::LastParameter is used to obtain the ending parameter of the curve.
AMCAX::Geom3Curve::Value or AMCAX::Geom3Curve::D0 is used for evaluation, while AMCAX::Geom3Curve::D1, AMCAX::Geom3Curve::D2, AMCAX::Geom3Curve::D3, and AMCAX::Geom3Curve::DN are used for differentiation.
AMCAX::Geom3Curve::Type is used to obtain the type of the curve, such as line, circle, ellipse, parabola, etc. The curve types can be referred to the enumeration class CurveType.
AMCAX::Geom3Curve::IsClosed is used to determine if the curve is closed (the starting point and the ending point are the same), and AMCAX::Geom3Curve::IsPeriodic is used to determine if the curve is periodic.
AMCAX::Geom3Curve::Reverse is used to reverse the Geom3Curve, modifying itself, while AMCAX::Geom3Curve::Reversed is used to obtain a reversed Geom3Curve without altering the original. After reversal, the starting and ending points of the curve are swapped. For general curves, the parameter range of the curve remains unchanged, whereas for trimmed curves, the parameter range may change. For example, a trimmed line originally with a parameter range from -1 to 3 will have a parameter range from -3 to 1 after reversal.

Here, we explain why the parameter range of the trimmed line changes to -3 to 1 after reversal. This is because when reversing a trimmed curve, the reversal is first applied to its basis curve (an infinitely long line), and then the parameters of the reversed starting and ending points are used to determine the parameter range after reversal.
Additionally, if you want to calculate the symmetric parameter for a given parameter, you can use AMCAX::Geom3Curve::ReversedParameter to achieve this.
Geom3Line is an infinitely long 3D line defined by a Point3 and a Direction3. The parameter at the Point3 is 0.0, and the parameter is positive in the direction of Direction3, with the parameter varying consistently with the length. The parameter domain of the line is infinite.

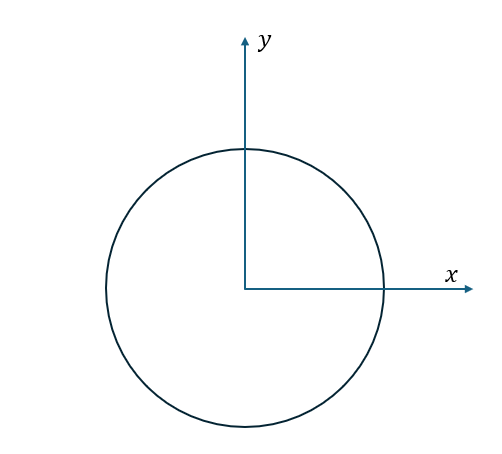
Geom3Circle is a circle in 3D space, defined by a frame and a radius, i.e., a standard circle on the XOY plane of the frame (with the center at the origin of the frame, and a point on the circle lying on the x-axis when the parameter is 0, rotating counterclockwise as the parameter increases). The parameter domain of the circle is [0, 2*pi), representing the parametric coordinates of the circle.
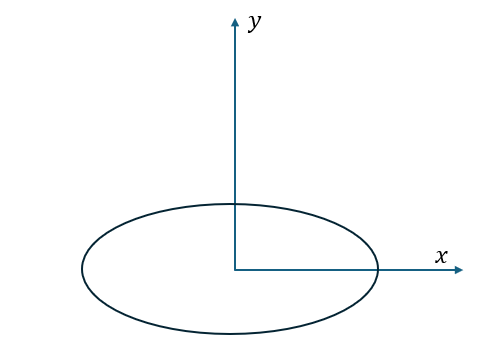
Geom3Ellipse is an ellipse in 3D space, defined by a frame and its major and minor radii, i.e., a standard ellipse on the XOY plane of the frame (with the center at the origin of the frame, and a point on the ellipse lying on the x-axis when the parameter is 0, rotating counterclockwise as the parameter increases). The parameter domain of the ellipse is [0, 2*pi), representing the parametric coordinates of the ellipse.
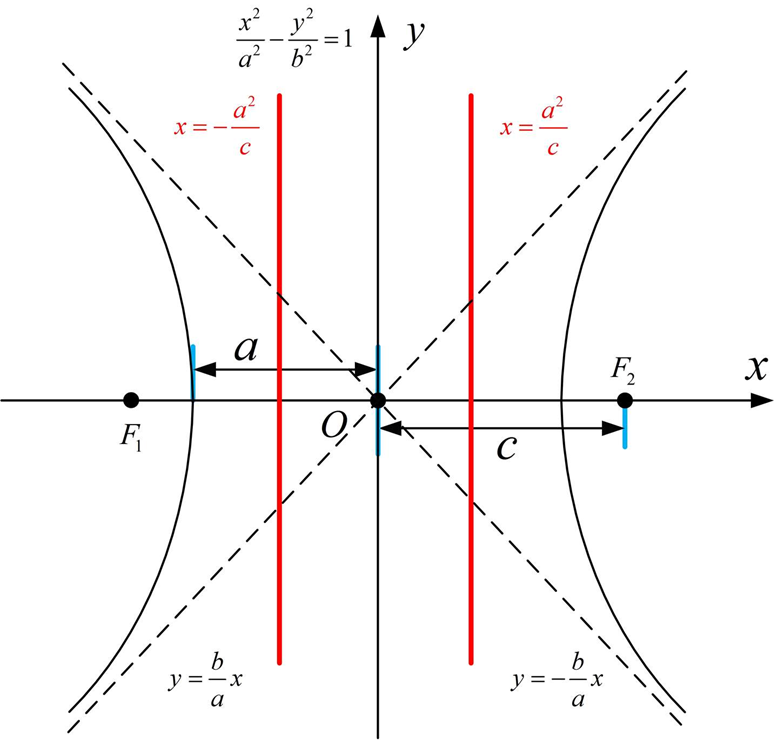
Geom3Hyperbola represents the right branch of a hyperbola in 3D space, defined by a frame and the radii of the real and imaginary axes, i.e., the right branch of a standard hyperbola on the XOY plane of the frame (with the center at the origin of the frame, and a point on the hyperbola lying on the positive half of the x-axis when the parameter is 0, rotating counterclockwise as the parameter increases, and the y-coordinate on the XOY plane becoming larger as the parameter increases). If you want to obtain the left branch of the hyperbola, you can use AMCAX::Geom3Hyperbola::OtherBranch. The parameter domain of the hyperbola is [-∞, +∞], representing the parametric coordinates of the hyperbola.
Geom3Parabola is a parabola in 3-dimensional space, defined by a reference frame and focal distance. Specifically, it is the standard parabola in the XOY plane of the reference frame (with the vertex at the origin of the reference frame, the axis of symmetry along the x-axis, and a parameter of 0 corresponding to a point on the parabola at the origin). As the parameter increases, the point moves along the parabola, and the y-coordinate on the XOY plane increases with larger parameter values. The domain of the parameter for the parabola is [-∞, +∞], representing the parameter coordinates of the parabola.
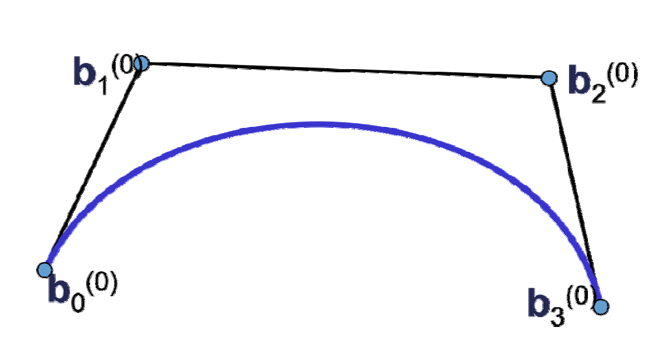
Geom3BezierCurve is a Bezier curve in 3D space, defined by control points and optional weights. The degree of the curve is one less than the number of control points; for example, if there are 4 control points, the curve is a cubic Bezier curve. Additionally, the parameter domain of the Bezier curve is [0,1]. When the parameter t=0, the curve is at the starting point (the first control point), and when t=1, the curve is at the ending point (the last control point). For a standard Bezier curve, its knot vector is {0, 1}, and the multiplicity of each knot is the degree plus one.
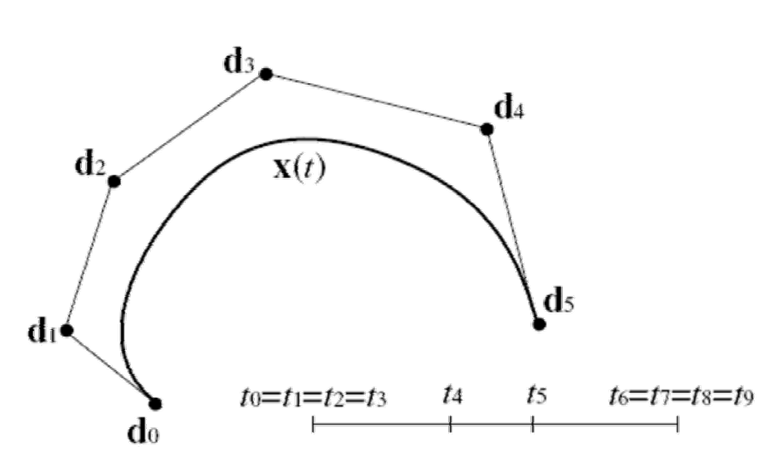
Geom3BSplineCurve is a BSpline curve in 3D space, defined by control points, a knot vector, knot multiplicities, and optional weights.
Geom3TrimmedCurve is a trimmed curve in 3D space, consisting of the original curve and two trimming parameters. It should be noted that the trimmed curve is always non-periodic, even if the trimming is done on a circle with the parameters [0, 2pi]. Additionally, periodic curves can be trimmed beyond their defined domain, such as with a circle.
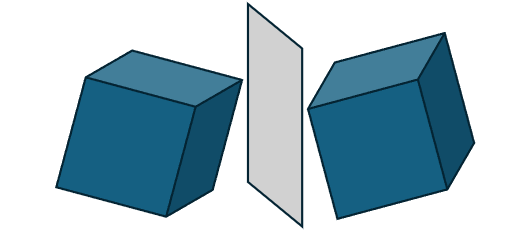
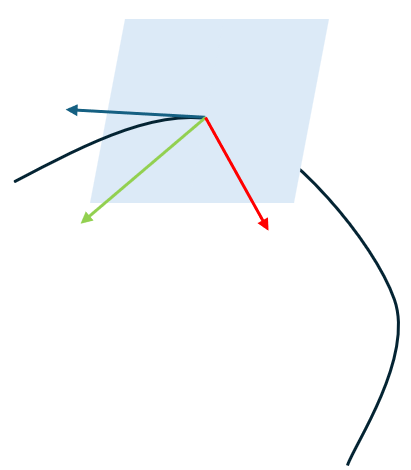
Geom3OffsetCurve is an offset curve in 3D space, composed of the original curve, offset distance, and reference direction. Its function is to offset the original curve by a specified distance in a direction perpendicular to the tangent, with the offset direction being the cross product of the tangent and the reference direction, as shown in the figure below. Here, the blue arrow represents the tangent, the green arrow represents the reference direction, and the red arrow represents the cross product direction, which is the offset direction.
Taking a standard circle on the xoy plane as an example, when the reference direction is oz, the offset direction is outward. Below is the result after offsetting:
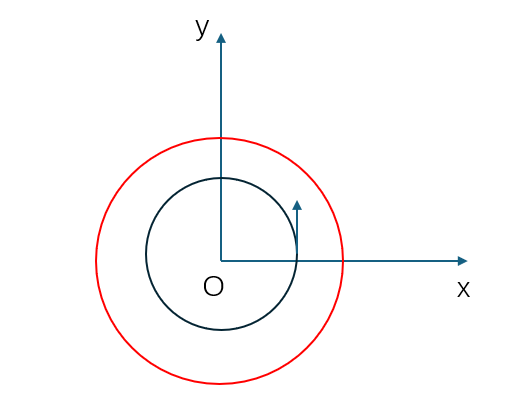
Additionally, if you want to obtain the original curve of the offset curve, you can use AMCAX::Geom3OffsetCurve::BasisCurve.
AMCAX::Geom2Curve::FirstParameter is used to obtain the starting parameter of the curve, and AMCAX::Geom2Curve::LastParameter is used to obtain the ending parameter of the curve.
AMCAX::Geom2Curve::Value or AMCAX::Geom2Curve::D0 are used for evaluation, while AMCAX::Geom2Curve::D1, AMCAX::Geom2Curve::D2, AMCAX::Geom2Curve::D3, AMCAX::Geom2Curve::DN are used for differentiation.
AMCAX::Geom2Curve::Type is used to obtain the type of the curve, such as line, circle, ellipse, parabola, etc. Curve types can be referenced from the enum class CurveType.
AMCAX::Geom2Curve::IsClosed is used to determine whether the curve is closed (whether the start and end points are the same), and AMCAX::Geom2Curve::IsPeriodic is used to determine if the curve is periodic.
AMCAX::Geom2Curve::Reverse is used to reverse the Geom2Curve and change it, while AMCAX::Geom2Curve::Reversed returns the reversed Geom2Curve without modifying the original. After reversing, the start and end points of the curve are swapped. For general curves, the parameter range remains unchanged, but for trimmed curves, the parameter range might change. For example, a trimmed line with a parameter range from -1 to 3 will have its range reversed to -3 to 1.
Here, we explain the reason why the parameter range of a trimmed line changes from -3 to 1 after reversal. This is because, when reversing a trimmed curve, it first reverses its basiscurve (the infinitely long line) and then determines the reversed parameter range based on the start and end parameters of the trimmed curve.
Additionally, to calculate the symmetric parameter for a given parameter, you can use AMCAX::Geom2Curve::ReversedParameter:
Except for Geom2OffsetCurve, the others are similar to their 3D counterparts.
Geom2Line is an infinitely long 2D line defined by a Point2 and a Direction2. The parameter at Point2 is 0.0, and the parameter increases in the direction of Direction2. The parameter variation corresponds to the length variation. The parameter domain of the line is infinite.
Geom2Circle is a circle in 2D space, defined by a frame and a radius. It represents a standard circle in the XOY plane of the frame (the center at the frame origin, the point on the x-axis when the parameter is 0, and the point rotates counterclockwise as the parameter increases). The parameter domain of the circle is [0, 2*pi), representing the parametric coordinates of the circle.
Geom2Ellipse is an ellipse in 2D space, defined by a frame and the major and minor radii. It represents a standard ellipse in the XOY plane of the frame (the center at the frame origin, the point on the x-axis when the parameter is 0, and the point rotates counterclockwise as the parameter increases). The parameter domain of the ellipse is [0, 2*pi), representing the parametric coordinates of the ellipse.
Geom2Hyperbola is the right branch of a hyperbola in 2D space, defined by a frame and the radii of the real and imaginary axes. It represents the right branch of a standard hyperbola in the XOY plane of the frame (the center at the frame origin, the point on the positive x-axis when the parameter is 0, and the point moves along the right branch of the hyperbola as the parameter increases. As the parameter increases, the y-coordinate in the XOY plane also increases). To obtain the left branch of the hyperbola, you can use AMCAX::Geom2Hyperbola::OtherBranch. The parameter domain of the hyperbola is [-∞, +∞], representing the parametric coordinates of the hyperbola.
Geom2Parabola is a parabola in 2D space, defined by a frame and the focal distance. It represents a standard parabola in the XOY plane of the frame (the vertex at the frame origin, with the axis of symmetry along the x-axis, the point at the origin when the parameter is 0, and the point moves along the parabola as the parameter increases. As the parameter increases, the y-coordinate in the XOY plane also increases). The parameter domain of the parabola is [-∞, +∞], representing the parametric coordinates of the parabola.
Geom2BezierCurve is a Bezier curve in 2D space, defined by control points and optional weights. The degree of the curve is the number of control points minus one; for example, with 4 control points, the curve is a 3rd degree Bezier curve. The parameter domain of a Bezier curve is [0,1]. When the parameter t = 0, the curve is at the start point (the first control point), and when t = 1, the curve is at the endpoint (the last control point). For standard Bezier curves, the node vector is {0, 1}, and the multiplicity of each node is the degree + 1.
Geom2BSplineCurve is a B-Spline curve in 2D space, defined by control points, knots, knot multiplicities, curve degree, and optional weights.
Geom2TrimmedCurve is a trimmed curve in 2D space, defined by an original curve and two trimming parameters. Similar to 3D, the trimmed curve is always non-periodic, and periodic curves can be trimmed beyond the domain. For example, for a circle:
Geom2OffsetCurve is an offset curve in 2D space, defined by the original curve and an offset distance. The offset direction is a 90° clockwise rotation of the tangent. Additionally, to obtain the original curve of the offset curve, you can use AMCAX::Geom2OffsetCurve::BasisCurve .
Bounds() gets the full parameter range. FirstUParameter() gets the starting U parameter, LastUParameter() gets the ending U parameter, FirstVParameter() gets the starting V parameter, and LastVParameter() gets the ending V parameter.
Use Value or D0 to evaluate, and D1, D2, D3, DN to get derivatives.
Type() gets the type, such as plane, sphere, etc.
IsUClosed() gets the closure in the U direction, IsUPeriodic() gets the periodicity in the U direction, IsVClosed() gets the closure in the V direction, IsVPeriodic() gets the periodicity in the V direction.
UReverse() reverses the U direction, and VReverse() reverses the V direction. After reversing, the starting and ending parameters of U and V will not change, only the coordinates will be flipped.
Additionally, UReversedParameter(t) computes the symmetric parameter of t in the u direction, while VReversedParameter(t) computes the symmetric parameter of t in the v direction.
UIso() returns the u iso-parameteric curve, which is the spatial curve corresponding to a straight line u = u0 in the parameter domain, and VIso() returns the v iso-parametric curve, which is the spatial curve corresponding to a straight line v = v0 in the parameter domain.
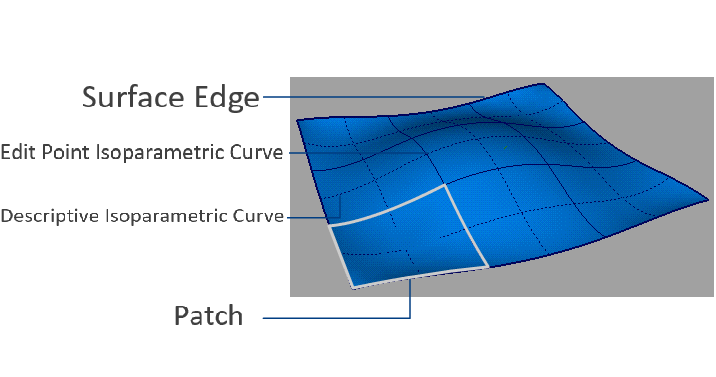
In the above example, the UIso is a line parallel to the Z-axis located on the side of the cylinder, and the VIso is a circle with radius r = 2.0 located at height v = 2.0.
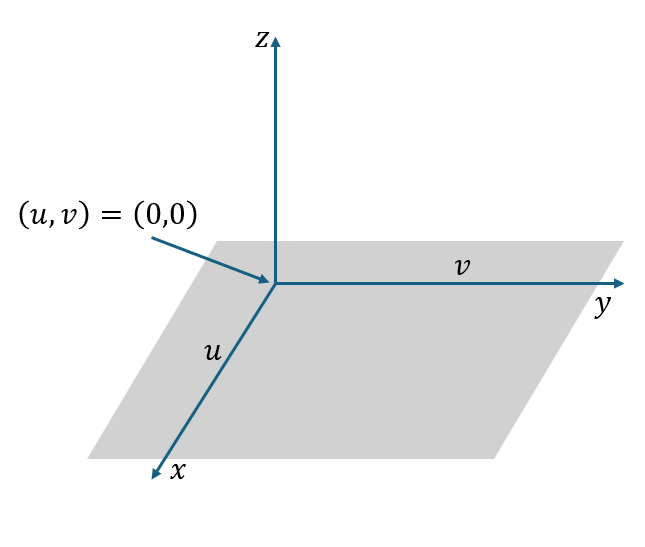
Geom3Plane is a plane in 3D space with an infinite parameter domain. The plane can be created based on AMCAX::Frame3, with the XOY plane as the surface and the OZ axis as the normal. The u direction corresponds to the OX direction, and the v direction corresponds to the OY direction. The 3D space point at (u, v) = (0, 0) is the origin of the Frame3 coordinate system.
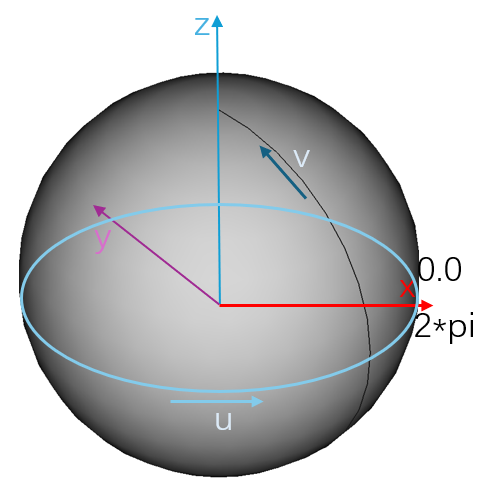
Geom3SphericalSurface is a sphere in 3D space with a parameter domain of [0, 2π) x [-π/2, π/2]. The parameters correspond to spherical coordinates. The sphere can be created using AMCAX::Frame3 and a radius. The origin of Frame3 is the center of the sphere. The circle in the XOY plane corresponds to an iso-parameteric curve with v = 0, while the semicircle in the XOZ plane corresponds to the iso-parameteric curve with u = 0. The positive u direction corresponds to a rotation of the OX axis towards the OY axis, and the positive v direction corresponds to a rotation from -OZ to OZ.
Geom3CylindricalSurface is a cylindrical surface (infinite length) in 3D space with a parameter domain of [0, 2π) x [-∞, ∞]. The parameters correspond to cylindrical coordinates. The cylinder surface can be created using AMCAX::Frame3 and a radius. The circle in the XOY plane corresponds to an iso-parameteric curve with v = 0. The positive u direction corresponds to a rotation from the OX axis towards the OY axis, while the v direction corresponds to the positive z direction. The change in v corresponds to the change in arc length.
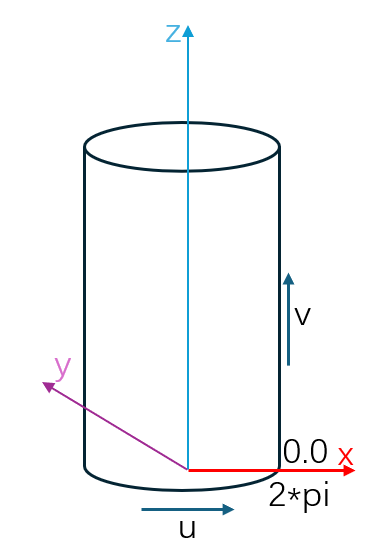
Geom3ConicalSurface is a conical surface (infinite length) in 3D space with a parameter domain of [0, 2π) x [-∞, ∞]. The conical surface can be created using Frame3, the radius of the circle in the XOY plane, and the half-angle. The circle in the XOY plane corresponds to an iso-parameteric curve with v = 0. The positive u direction corresponds to a rotation from the OX axis towards the OY axis, while the positive v direction corresponds to an inclined line, forming an acute angle with the z direction.
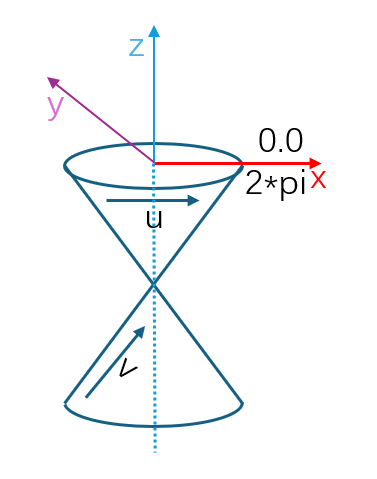
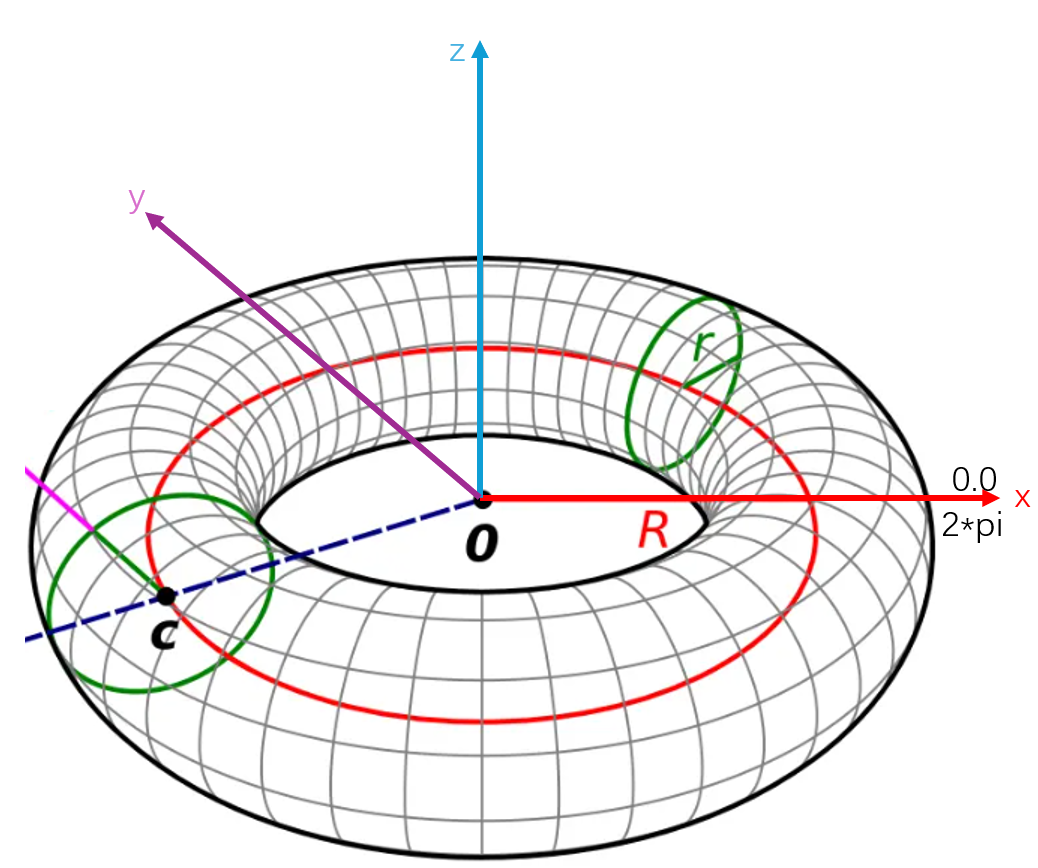
Geom3ToroidalSurface is a toroidal surface (doughnut shape) in 3D space with a parameter domain of [0, 2π) x [0, 2π]. The toroidal surface can be created using Frame3, the large radius, and the small radius. The standard circle in the XOY plane corresponds to an iso-parameteric curve with v = 0, while the standard circle in the XOZ plane corresponds to an iso-parameteric curve with u = 0.
Geom3BezierSurface is a Bezier surface in 3D space with a parameter domain of [0, 1] x [0, 1]. The Bezier surface can be created using control points and optional weights. When creating it, make sure the number of weights matches the number of control points. If all weights are equal (e.g., all equal to 1), the rational Bezier surface degenerates into a standard Bezier surface.
Geom3BSplineSurface is a B-Spline surface in 3D space. The B-Spline surface can be created based on control points, knot vectors, knot multiplicities, and curve degrees. The following conditions must be met when creating it: The length of UKnots = the length of UMultiplicities; The length of VKnots = the length of VMultiplicities;sum(UMultiplicities) = Poles.Rows() + UDegree + 1;sum(VMultiplicities) = Poles.Cols() + VDegree + 1;The knot vectors must be monotonically increasing, and the multiplicity of each knot cannot exceed the degree of the curve.
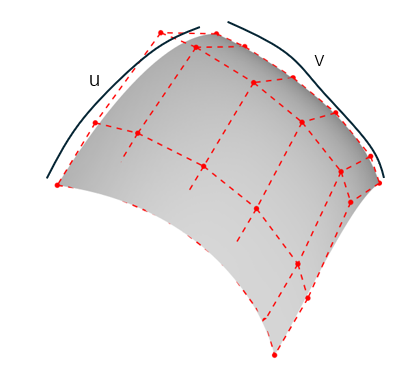
Geom3SurfaceOfExtrusion is an extrusion surface (stretch surface) in 3D space (infinite), which can be created based on a base curve (Geom3Curve) and extrusion direction. The u-direction is the parameter direction of the base curve, and the v-direction is the extrusion reverse. The isoparametric line v=0 corresponds to the base curve, and any u-isoparametric line is a straight line. The u parameter domain corresponds to the base curve's parameter domain, while the v parameter domain is infinite.
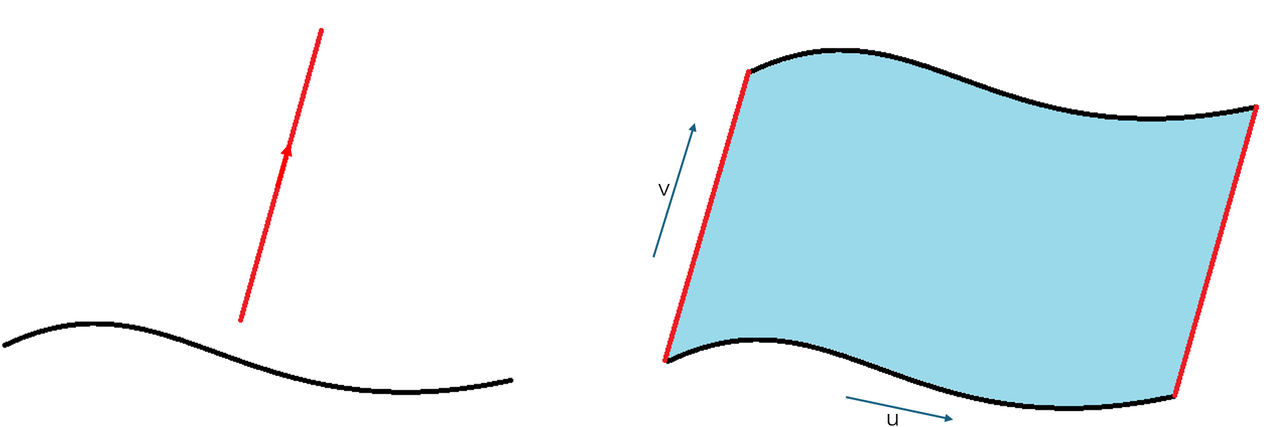
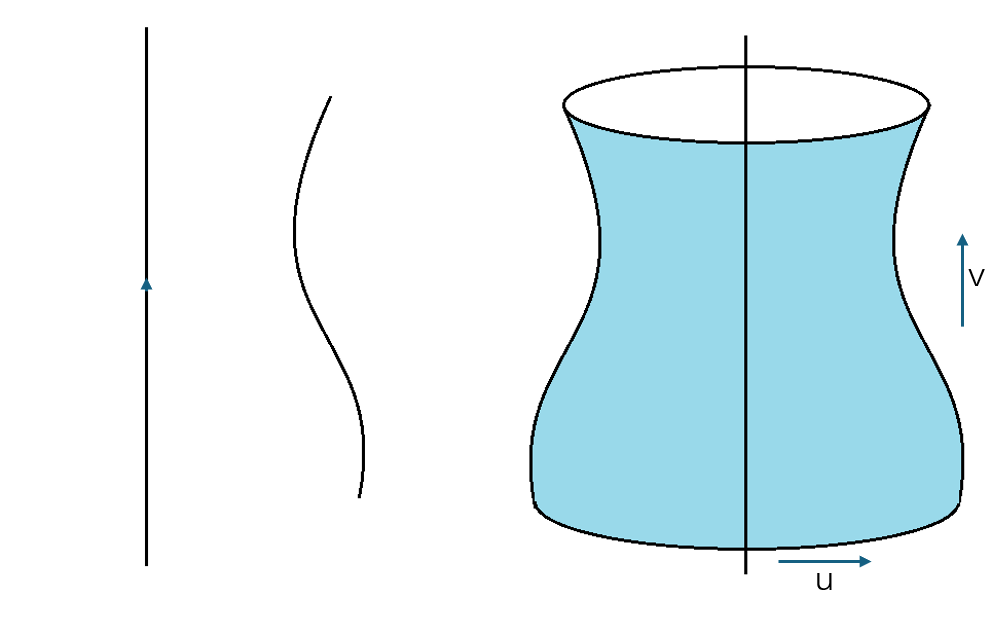
Geom3SurfaceOfRevolution is a surface of revolution in 3D space. It can be created based on a base curve (Geom3Curve) and an axis of rotation. The u parameter domain is [0, 2π), and the v parameter domain is the domain of the base curve. Each v-isoparametric line is a circle with its center on the rotation axis, and each u-isoparametric line can be generated by rotating the base curve around the axis.
Geom3TrimmedSurface is a trimmed surface in 3D space, created from an original surface with trimming parameters. You can trim in the u-direction, v-direction, or both u and v directions. To access the original surface, you can use AMCAX::Geom3TrimmedSurface::BasisSurface.
Geom3OffsetSurface is an offset surface in 3D space, which moves every point of the original surface along its normal direction by a certain distance. To access the original surface, you can use AMCAX::Geom3OffsetSurface::BasisSurface.
To obtain the equivalent surface after offsetting, such as a sphere or cylinder, you can use AMCAX::Geom3OffsetSurface::Surface.
In fact, all the offset surfaces (plane, sphere, cylinder, cone, torus, extrusion, revolution, Bezier, BSpline) mentioned above can be represented by the original surface type. However, only equivalent surfaces of trimmed or non-trimmed planes, cylinders, cones, spheres, and tori are implemented, while the others will return a null pointer.