Geometry Foundation

Coord

Construction

Using the default constructor will result in the origin of coordinates. You need to input floating-point numbers when constructing. Also, all geometries only support input of floating-point numbers, which will not be specifically mentioned in the future.

Coord3（Three-Dimensional Coordinate）

AMCAX::Coord3 crd1(0.0, 0.0, 2.0);

Coord2（Two-Dimensional Coordinate）

AMCAX::Coord2 crd2d(0.0,1.0);

Get and Modify

Get

You can use the following two methods to get the value of a particular dimension of the coordinate.

AMCAX::Coord3 crd(0.0, 1.0, 2.0);
double x = crd.X();
double y = crd.Y();
double z = crd.Z();
 
double x2 = crd[0];
double y2 = crd[1];
double z2 = crd[2];

Modify

You can modify the value of a particular dimension of the coordinate using the following two methods.

AMCAX::Coord3 crd(0.0, 1.0, 2.0);
crd.SetXYZ(1.0, 0.0, 2.1);
 
crd.SetX(0.5);
crd.SetY(0.5);
crd.SetZ(0.5);

Common Function

Operation

Support addition, subtraction, scalar multiplication, dot product, cross product, and also support == and !=.

Addition and Subtraction

AMCAX::Coord3 crd1(2.0, 1.0, 2.0);
AMCAX::Coord3 crd2(0.2, 1.0, 1.0);
//+
AMCAX::Coord3 crd3 = crd1 + crd2;
//-
AMCAX::Coord3 crd4 = crd1 - crd2;

Scalar Multiplication

AMCAX::Coord3 crd5 = crd1 * 0.5;

Dot Product

double t = crd1.Dot(crd2);

Cross Product

AMCAX::Coord3 crd6 = crd1.Cross(crd2);

== and !=

== and != can be used to compare coordinates and their respective dimensions.

double result1 = crd1 == crd2;
std::cout << result1 << std::endl;
double result2 = crd1 != crd2;
std::cout << result2 << std::endl;
double result3 = crd1.Y() == crd2.Y();
std::cout << result3 << std::endl;

Norm

The kernel support calculating the norm (magnitude) of the coordinate and normalizing the coordinate.

Magnitude

double length = crd1.Norm();

Normalization

There are two ways to normalize a coordinate: one does not change the coordinate itself and creates a new coordinate, while the other directly modifies the coordinate.

AMCAX::Coord3 crd2 = crd.Normalized();
 
//change
crd.Normalize();

Output and Input

The kernel support outputting coordinates using << and inputting with >>.

Output

std::cout << crd1 << std::endl;

Input

AMCAX::Coord3 crd7;
std::istringstream is("0.0 1.0 2.0");
is >> crd7;

Point

Construction

Using the default constructor will result in the origin. It can either be directly created or constructed based on Coord3/Coord2.

Coord3（Three-Dimensional Point）

AMCAX::Point3 p1(0.0, 1.0, 2.0);
 
AMCAX::Coord3 crd1(0.0, 1.0, 2.0);
AMCAX::Point3 p2(crd1);

Coord2（Two-Dimensional Point）

AMCAX::Point2 p3(0.0, 1.0);
 
AMCAX::Coord2 crd2(0.0, 1.0);
AMCAX::Point2 p4(crd2);

Get and Modify

Get

You can use the following two methods to get the value of a particular dimension of the point.

AMCAX::Point3 p1(0.0, 1.0, 2.0);
double x = p1.X();
double y = p1.Y();
double z = p1.Z();
 
double x2 = p1[0];
double y2 = p2[1];
double z2 = p3[2];

Modify

You can modify the value of a particular dimension of the point using the following two methods.

AMCAX::Point3 p1(0.0, 1.0, 2.0);
p1.SetCoord(1.0, 0.0, 2.1);
 
p1.SetX(0.5);
p1.SetY(0.5);
p1.SetZ(0.5);

Common Function

Operation

The kernel does not support arithmetic operations (addition, subtraction, multiplication, division) on points. In fact, most geometries do not support arithmetic operations, except for Coord. This will not be explained further. However, if you need to perform arithmetic on points, you can first obtain the point's Coord, then perform operations on the Coord:

AMCAX::Point3 p1(0.0, 1.0, 2.0);
AMCAX::Point3 p2(1.0, 2.0, 2.0);
const Coord3& crd3 = p1.Coord();
const Coord3& crd4 = p2.Coord();
const Coord3& crd5 = crd3 + crd4;
AMCAX::Point3 p3(crd5);

Calculate the Distance Between Two Points

AMCAX::Point3 p1(0.0, 1.0, 2.0);
AMCAX::Point3 p2(1.0, 2.0, 2.0);
double dis = p1.Distance(p2);

Transformation

Most geometries support transformations such as translation, rotation, mirror, and scale, which will not be explained further.

Translation Transformation

AMCAX::TopoShape box = AMCAX::MakeBox(AMCAX::Point3(-5.0, -5.0, 0.0), AMCAX::Point3(5.0, 5.0, 3.0));
AMCAX::Transformation3 trans;
trans.SetTranslation(AMCAX::Vector3(1.0, 0.0, 0.0));
AMCAX::TopoShape box2 = AMCAX::TransformShape(box, trans);

Rotation Transformation

AMCAX::TopoShape box = AMCAX::MakeBox(AMCAX::Point3(-5.0, -5.0, 0.0), AMCAX::Point3(5.0, 5.0, 3.0));
AMCAX::Transformation3 trans;
trans.SetRotation(AMCAX::Axis3(), M_PI * 0.25);
AMCAX::TopoShape box3 = AMCAX::TransformShape(box, trans);

Mirror Transformation

Point Mirror

AMCAX::TopoShape box = AMCAX::MakeBox(AMCAX::Point3(-5.0, -5.0, 0.0), AMCAX::Point3(5.0, 5.0, 3.0));
AMCAX::Transformation3 trans;
trans.SetMirror(AMCAX::Point3(10.,10.,10.));
AMCAX::TopoShape box4 = AMCAX::TransformShape(box, trans);

Axis Mirror

AMCAX::TopoShape box = AMCAX::MakeBox(AMCAX::Point3(-5.0, -5.0, 0.0), AMCAX::Point3(5.0, 5.0, 3.0));
AMCAX::Transformation3 trans;
trans.SetMirror(AMCAX::Axis3(AMCAX::Point3(10.0, 20.0, 30.0), AMCAX::Direction3(0.0, 1.0, 1.0)));
AMCAX::TopoShape box5 = AMCAX::TransformShape(box, trans);

Plane Mirror

AMCAX::TopoShape box = AMCAX::MakeBox(AMCAX::Point3(-5.0, -5.0, 0.0), AMCAX::Point3(5.0, 5.0, 3.0));
AMCAX::Transformation3 trans;
trans.SetMirror(AMCAX::Frame3(AMCAX::Point3(10.0, 10.0, 10.0), AMCAX::Direction3(0.0, 0.0, 1.0)));
AMCAX::TopoShape box6 = AMCAX::TransformShape(box, trans);

Uniform Scale Transformation

AMCAX::TopoShape box = AMCAX::MakeBox(AMCAX::Point3(-5.0, -5.0, 0.0), AMCAX::Point3(5.0, 5.0, 3.0));
AMCAX::Transformation3 trans;
trans.SetScale(AMCAX::Point3(), 0.5);
AMCAX::TopoShape box7 = AMCAX::TransformShape(box, trans);

Composite Transformation

The formula for composite transformation is sRx+bsRx+b, where ss is the scaling factor, RR is the rotation matrix, xx is the coordinate to be transformed, and bb is the translation vector.

For example, constructing the following transformation: first rotate around the x-axis by π/4π/4, then scale by a factor of 0.2, and finally translate 1 unit along the x-axis:

AMCAX::TopoShape box = AMCAX::MakeBox(AMCAX::Point3(-5.0, -5.0, 0.0), AMCAX::Point3(5.0, 5.0, 3.0));
AMCAX::Transformation3 trans;
trans.SetRotationPart(AMCAX::QuaternionT<double>(AMCAX::Coord3(1.0, 0.0, 0.0), M_PI * 0.25));
trans.SetScaleFactor(0.2);
trans.SetTranslationPart(AMCAX::Vector3(1.0, 0.0, 0.0));
AMCAX::TopoShape box8 = AMCAX::TransformShape(box, trans);

Transforming an Object from Local Coordinate System to Global (or Another Coordinate System)

Construct a transformation so that the object in the local coordinate system f2={O=(1,0,0), OZ=(1,1,0), OX=(0,0,1)}is transformed to the global coordinate system:

AMCAX::Frame3 f1;
AMCAX::Frame3 f2(AMCAX::Point3(1.0, 0.0, 0.0), AMCAX::Direction3(0.5, 0.5, 0.0), AMCAX::Direction3(0.0, 0.0, 1.0));
AMCAX::Transformation3 trans1;
trans1.SetTransformation(f2, f1);

Transforming Frame 1 by Translating and Rotating to Frame 2

Construct a transformation to change the global coordinate frame to another frame f2={O=(1,0,0), OZ=(1,1,0), OX=(0,0,1)}：

AMCAX::Frame3 f1;
AMCAX::Frame3 f2(AMCAX::Point3(1.0, 0.0, 0.0), AMCAX::Direction3(0.5, 0.5, 0.0), AMCAX::Direction3(0.0, 0.0, 1.0));
AMCAX::TopoShape box11 = AMCAX::MakeBox(f1, 2.0, 2.0, 2.0);
AMCAX::Transformation3 trans2;
trans2.SetDisplacement(f1, f2);
AMCAX::TopoShape box12 = AMCAX::TransformShape(box11, trans2);

Multiplying Transformations

trans1 * trans2。which applies trans2 first, then trans1:

AMCAX::TopoShape box = AMCAX::MakeBox(AMCAX::Point3(-5.0, -5.0, 0.0), AMCAX::Point3(5.0, 5.0, 3.0));
AMCAX::Transformation3 trans11;
trans11.SetScaleFactor(0.2);
AMCAX::Transformation3 trans22;
trans22.SetMirror(AMCAX::Point3(10., 10., 10.));
AMCAX::TopoShape bbox = AMCAX::TransformShape(box, trans11*trans22);

Vector and Direction

Vector3 refers to a mathematical vector with both direction and length, while Direction3 has only direction, with a magnitude of 1.0.

Construction

AMCAX::Vector3 vec; // (0.0,0.0,0.0)
AMCAX::Direction3 dir; // (1.0, 0.0, 0.0)
std::cout << vec << ' ' << dir << std::endl;
 
AMCAX::Vector3 vec1(0.1, 2.0, -3.3);
AMCAX::Direction3 dir1(0.1, 2.0, -3.3); // automatically normalized
std::cout << vec1 << ' ' << dir1 << std::endl;
 
AMCAX::Vector3 vec2(dir1);
AMCAX::Direction3 dir2(vec1);
std::cout << vec2 << ' ' << dir2 << std::endl;
 
AMCAX::Point3 p1(0.0, 0.0, 0.0);
AMCAX::Point3 p2(1.0, 0.0, 0.0);
AMCAX::Vector3 vec3(p1, p2); // build vector P1P2
std::cout << vec3 << std::endl;

Get and Modify

The access and modification methods for vectors and directions are similar to the Coord class, except that directions are automatically normalized.

Get

To get a particular dimension's value of a vector or direction:

AMCAX::Vector3 vec; // (0.0,0.0,0.0)
AMCAX::Direction3 dir; // (1.0, 0.0, 0.0)
//vector
double x = vec.X();
double y = vec.Y();
double z = vec.Z();
 
double x2 = vec[0];
double y2 = vec[1];
double z2 = vec[2];
 
//direction
double x3 = dir.X();
double y3 = dir.Y();
double z3 = dir.Z();
 
double x4 = dir[0];
double y4 = dir[1];
double z4 = dir[2];

Modify

To modify a particular dimension's value of a vector or direction:

//vector
vec.SetCoord(0.1, 2.0, -3.3);
 
vec.SetX(0.1);
vec.SetY(2.0);
vec.SetZ(-3.3);
 
//direction
dir.SetCoord(0.1, 2.0, -3.3);
 
dir.SetX(0.1);
dir.SetY(2.0);
dir.SetZ(-3.3);

Common Operation

Operation

Vectors can be added, subtracted, and scaled by a number. Directions do not support addition and subtraction. Both vectors and directions support dot and cross products, similar to the Coord class.

Addition and Subtraction

AMCAX::Vector3 vec1(0.1, 2.0, -3.3);
AMCAX::Vector3 vecc(2.1, 1.5, 2.3);
//+
AMCAX::Vector3 vecc1 = vecc + vec1;
//-
AMCAX::Vector3 vecc2 = vecc - vec1;

Scalar Multiplication

AMCAX::Vector3 vecc(2.1, 1.5, 2.3);
AMCAX::Vector3 vecc3 = vecc * 2.0;

Dot Product

//vector
AMCAX::Vector3 vec1(0.1, 2.0, -3.3);
AMCAX::Vector3 vecc(2.1, 1.5, 2.3);
double t = vecc.Dot(vec1);
 
//direction
AMCAX::Direction3 dir1(0.1, 2.0, -3.3);
AMCAX::Direction3 dirr(2.3, 1.6, 1.3);
double t2 = dirr.Dot(dir1);

Cross Product

//vector
AMCAX::Vector3 vec1(0.1, 2.0, -3.3);
AMCAX::Vector3 vecc(2.1, 1.5, 2.3);
AMCAX::Vector3 vecc4 = vecc.Cross(vec1);
 
//direction
AMCAX::Direction3 dir1(0.1, 2.0, -3.3);
AMCAX::Direction3 dirr(2.3, 1.6, 1.3);
AMCAX::Direction3 dirr2 = dirr.Cross(dir1);

Angle

The kernel supports computing angles. The Angle() method calculates the angle between vectors, with a range of [0.0, pi]. The AngleWithRef() method computes the angle with a reference direction in 2D, with a range of [-pi, pi]. The sign of the angle depends on whether the coordinate system is right-handed or left-handed.

AMCAX::Direction3 ddir(1.0, 0.0, 0.0), other_dir(0.0, 0.5, 0.5), ref_dir(0.0, 0.0, 1.0);
double angle1 = ddir.Angle(other_dir);
double angle2 = ddir.AngleWithRef(other_dir, ref_dir);

Note: In 2D, only Angle() should be used to calculate rotation.
Additionally, the methods IsOpposite() and IsParallel() can be used to check if vectors or directions are opposite or parallel:

//vector
AMCAX::VectorT<double, 3> v1(1.0, 2.0, 3.0);
AMCAX::VectorT<double, 3> v2(-1.0, -2.0, -3.0);
AMCAX::VectorT<double, 3> v3(2.0, 4.0, 6.0);
 
//IsOpposite
bool op1 = v1.IsOpposite(v2, 0.1);
std::cout << op1 << std::endl;
//IsParallel
bool pa1 = v1.IsParallel(v3, 0.1);
std::cout << pa1 << std::endl;
 
//direction
AMCAX::DirectionT<double, 3> d1(1.0, 2.0, 3.0);
AMCAX::DirectionT<double, 3> d2(-1.0, -2.0, -3.0);
AMCAX::DirectionT<double, 3> d3(2.0, 4.0, 6.0);
 
//IsOpposite
bool op2 = d1.IsOpposite(d2,0.1);
std::cout << op2 << std::endl;
//IsParallel
bool pa2 = d1.IsParallel(d3, 0.1);
std::cout << pa2 << std::endl;

Magnitude

Vector can compute their magnitude and be normalized, similar to the Coord class.

Magnitude

AMCAX::Vector3 vec1(0.1, 2.0, -3.3);
double length = vec1.Norm();

Normalization

AMCAX::Vector3 vec1(0.1, 2.0, -3.3);
AMCAX::Vector3 vn = vec1.Normalized();
//change
vec1.Normalize();

Axis

Axis3 is an axis in 3D space, equivalent to a Point3 plus a Direction3. Construction is as follows:

AMCAX::Point3 p;
AMCAX::Direction3 dir;
AMCAX::Axis3 axis(p, dir);
//get
AMCAX::Point3 p1 = axis.Location();
AMCAX::Direction3 dir1 = axis.Direction();

The kernel also supports computing the angle and magnitude of axis:

AMCAX::Point3 p;
AMCAX::Direction3 dir;
AMCAX::Axis3 axis(p, dir);
AMCAX::Axis3 axis2(AMCAX::Point3(1.0, 2.0, 3.0), AMCAX::Direction3(0.0, 1.0, 1.0));
 
double angle = axis.Angle(axis2);

Frame

Definition

Frame3 is a frame in 3D space, consisting of a point and three mutually perpendicular directions.

The world coordinate system {O; x, y, z} is a commonly used frame, and the default constructor of Frame3 creates this frame:

AMCAX::Frame3 frame;
const AMCAX::Point3& p = frame.Location();
//get
const AMCAX::Direction3& x = frame.XDirection();
const AMCAX::Direction3& y = frame.YDirection();
const AMCAX::Direction3& z = frame.Direction();
 
AMCAX::Frame3 frame2(p, z, x);

Note: If the input z-axis is not perpendicular to the x-axis, the algorithm will compute the y-axis as the cross product of z and x, and compute x as the cross product of y and z.

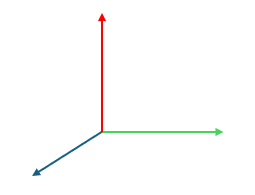
Right-Handed and Left-Handed Systems

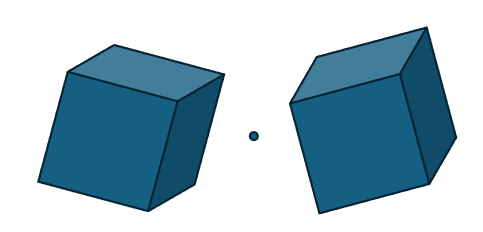
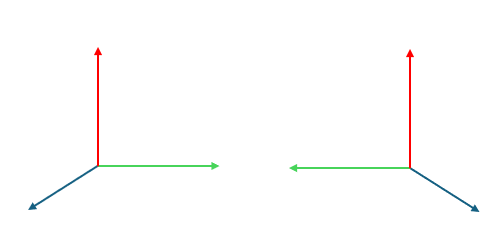
The left image shows a right-handed system, and the right image shows a left-handed system (with blue, green, and red representing the x, y, and z axes respectively). The most common local coordinate system is the right-handed system. To determine if a frame is right-handed, curl the fingers of the right hand from x to y, and if the thumb points in the z direction, it is a right-handed system.

The way we kernel to get whether a standard frame is right-handed or not is:

AMCAX::Frame3 frame;
bool isRightHand = frame.IsDirect();

Local Coordinate System

A frame can represent a local coordinate system, which simplifies the construction of spatial curves and surfaces.

Transformation

There are three main transformations: transforming from a local coordinate system to the global coordinate system, transforming from one local coordinate system to another, and constructing affine transformations to translate, rotate, or mirror one frame to another. Refer to the transformation section above for more details.